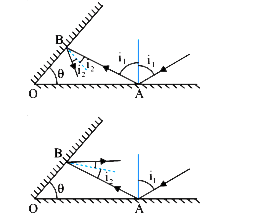
Two plane mirrors are inclined at angle $θ = 60^{\circ}$ with each-other. A ray of light strikes one of them. Find its deviation after it has been reflected twice-one from each mirror.

Text Solution

Verified by Experts

Case I:
$δ_{1}$ =clockwise deviation atA= $180^{\circ} - 2 i_{1}$
$δ_{2}$ anticlockwise deviation at B= $180^{\circ} - 2 i_{2}$
Now, from $Δ$ OAB, we have
angle O + angle A + angle B = $180^{\circ}$
$\Rightarrow i_{1} - i_{2} = θ$
As $i_{1} > i_{2}, δ_{1} < δ_{2}$
Hence, the net angle clockwise deviation= $δ_{2}$ - $δ_{1}$
$= (180^{\circ} - 2 i_{2}) - (180^{\circ} - 2 i_{1})$
$= 2 (i_{1} - i_{2}) = 2 θ = 120^{\circ}$
Case II:
$δ_{1}$ =clockwise deviation atA= $180^{\circ} - 2 i_{1}$
$δ_{2}$ anticlockwise deviation at B= $180^{\circ} - 2 i_{2}$
Now, from $Δ$ OAB, we have
angle O + angle A + angle B = $180^{\circ}$
or, $θ + (90^{\circ} - i_{1}) + (90^{\circ} - i_{2}) = 180^{\circ} \Rightarrow i_{1} + i_{2} = θ$
Hence, the net angle clockwise deviation= $δ_{2} + δ_{1}$
$= (180^{\circ} - 2 i_{2}) + (180^{\circ} - 2 i_{1}) = 360^{\circ} - 2 (i_{1} + i_{2}) = 360^{\circ} - 2 θ$
$\Rightarrow$ Net anti-clockwise deviation = $360^{\circ} - (360^{\circ} - 2 θ) = 2 θ = 120^{\circ}$

Updated on:21/07/2023

Two plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. Determine the angle between the two mirrors:
Aa $0^{\circ}$
B( b) $45^{\circ}$
Cc $60^{\circ}$
Dd $90^{\circ}$
Two plane mirrors are inclined at an angle $θ$ to one another A ray of light incident on the first mirror and parallel ot the second mirror is reflected from the second mirror parallel to the first mirror ,
What is the value of $θ$
A $0^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Two plane mirror are inclined to each other at $90^{\circ}$ . A ray of light is incident on one mirror. The ray will undergo a total deviation of
A $180^{\circ}$
B $90^{\circ}$
C $45^{\circ}$
Ddata insufficient