Through two points :

A unique line can be drawn

No line can be drawn

More than one line can be drawn

None of these

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the question "Through two points, how many lines can be drawn?", let's analyze the situation step by step.
Step 1: Identify the two points
Let's denote the two points as A and B. We will visualize these points on a plane.
Hint: Always start by clearly marking the points in your geometric problem.
Step 2: Understand the concept of a line
A line is defined as a straight path that extends infinitely in both directions. It is determined by two distinct points.
Hint: Remember that a line is uniquely defined by any two distinct points.
Step 3: Draw the line through the two points
Now, we can draw a line that connects point A and point B. This line can be represented as line AB.
Hint: When drawing, ensure that the line passes through both points without any breaks.
Step 4: Consider the uniqueness of the line
According to Euclid's postulates, through any two distinct points, there exists exactly one straight line. This means that no matter how we try to draw a line through points A and B, it will always be the same line.
Hint: Think about the definition of a line and how it relates to the points it connects.
Step 5: Conclusion
Since we can only draw one unique line through two distinct points, the correct answer to the question is that a unique line can be drawn through the two points.
Final Answer: A unique line can be drawn through two points.

Updated on:7/8/2024

A car is moving along a straight road with a uniform acceleration. It passes through two points P and Q separated by a distance with velocity $30 k m / h$ and $40 k m / h$ respectively. The velocity of the car midway between P and Q is
A $33.3 k m / h$
B $20 \sqrt{2} k m / h$
C $25 \sqrt{2} k m / h$
D $0.35 k m / h$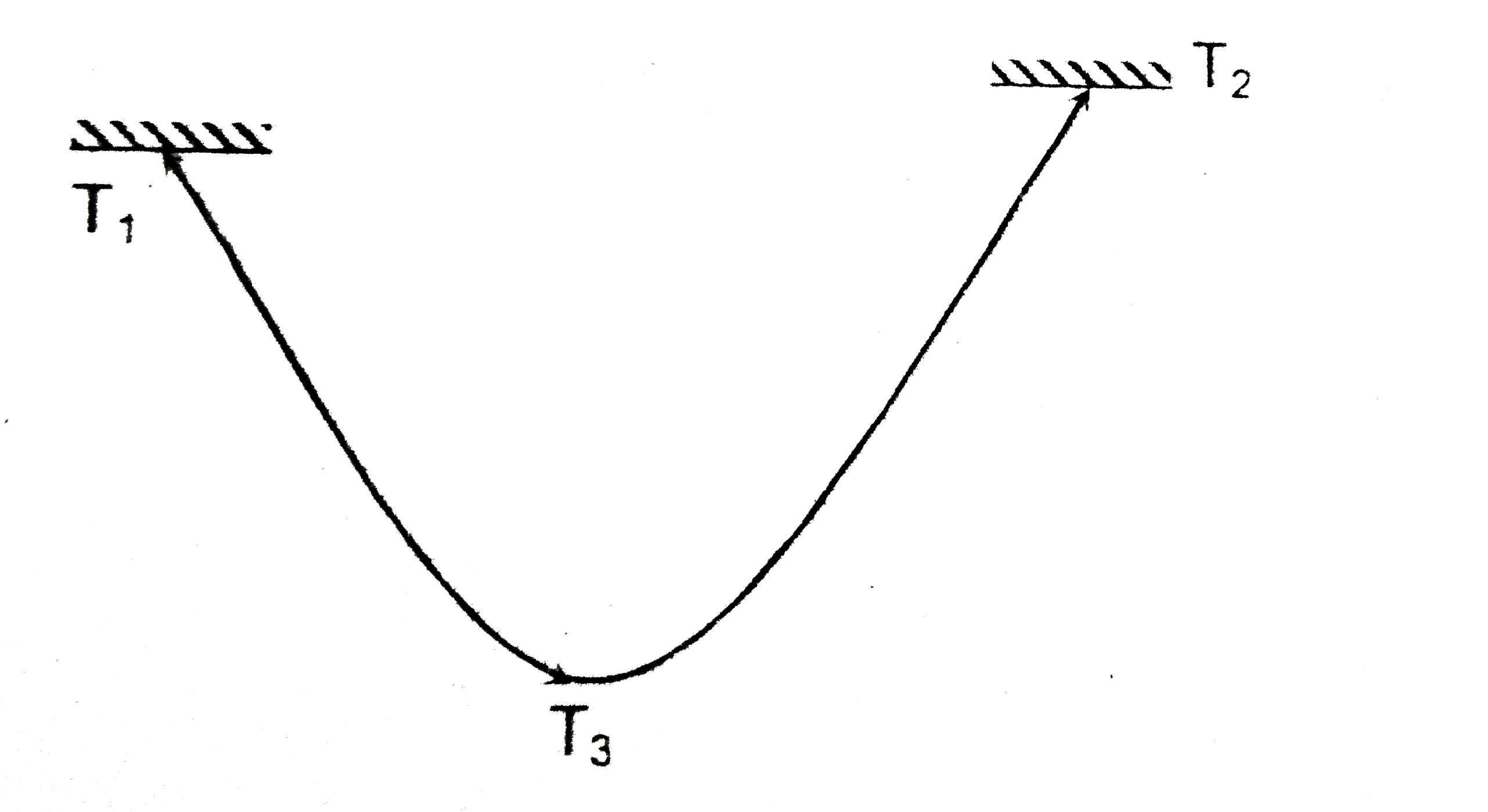
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are $T_{1}$ and $T_{2}$ and at the lowest point is $T_{3}$ . Mass of string in terms of $T_{1}, T_{2}$ and $T_{3}$ can be represented a (uniform gravity 'g' exists downwards)
A $\frac{\sqrt{T_{1}^{2} - T_{3}^{2}} + \sqrt{T_{2}^{2} - T_{3}^{2}}}{g}$
B $\frac{(T_{1} + T_{2} - 2 T_{3})}{g}$
C $\frac{\sqrt{T_{1}^{2} + T_{2}^{2}}}{g}$
D $\frac{\sqrt{T_{1}^{2} + T_{3}^{2}} + \sqrt{T_{2}^{2} + T_{3}^{2}}}{g}$
Equation of the plane passing through the two points A(1,2,-3), B(3,-4,-1), and parallel to the line $\frac{x + 1}{2} = \frac{4 - y}{3} = z - 5$ , is
Ay+3z+7=0
By-3z+7=0
Cx+3z+7=0
Dx-3z+7=0