A projectile is fired with velocity $v_{0}$ from a gun adjusted for a maximum range. It passes through two points $P and Q$ whose heights above the horizontal are $h$ each. Show that the separation of the two points is $\frac{v_{0}}{g} \sqrt{v_{0}^{2} - 4 g h})$ .

Video Solution

Text Solution

Verified by Experts

The trajectory of projectile is given by
$y = x tan θ - \frac{g x^{2}}{2 v_{0}^{2}} (1 + {tan}^{2} θ)$
Gun is adjusted for minimum range, therefore, $\propto = 45^{\circ}$
$y = x - \frac{g (x^{2})}{v_{0}^{2}}$
For $y = h$ , we have $h = x - \frac{g}{v_{0}^{2}} x^{2}$
$x^{2} - \frac{v_{0}^{2}}{g} x + \frac{v_{0}^{2}}{g} h = 0$
If $x_{1} and x_{2}$ are roots of the above equation,
$x_{1} + x_{2} = \frac{v_{0}^{2}}{g} \Rightarrow x_{1} x_{2} = \frac{v_{0}^{2}}{g} h$
${(x_{1} + x_{2})}_{1}^{2} = {(x_{1} + x_{2})}_{1}^{2} - 4 x_{1} x_{2} = (\frac{v_{0}^{2}}{g}) - 4 \frac{v_{0}^{2}}{g} h$
$x_{1} - x_{2} = \frac{v_{0}}{g} \sqrt{v_{0}^{2} - 4 g h}$ .

A projectile is fired with velocity $v_{0}$ from a gun adjusted for a maximum range.It passes through two points $P$ and $Q$ whose heights above the horizontal are $h$ each.The separation of the two points is
A $\frac{v_{0}}{g} \sqrt{v_{0}^{2} - 4 g h}$
B $\frac{v_{0}}{g} \sqrt{v_{0}^{2} + 4 g h}$
C $2 \frac{v_{0}}{g} \sqrt{v_{0}^{2} - 4 g h}$
D $\frac{v_{0}}{g} \sqrt{v_{0}^{2} - g h}$
At $t = 0$ a projectile is fired from a point $O$ (taken as origin) on the ground wita speed of $50 m / s$ at an angle of $53^{\circ}$ with the horizontal. It just passes two points $A$ and $B$ each at height $75 m$ above horizontal.

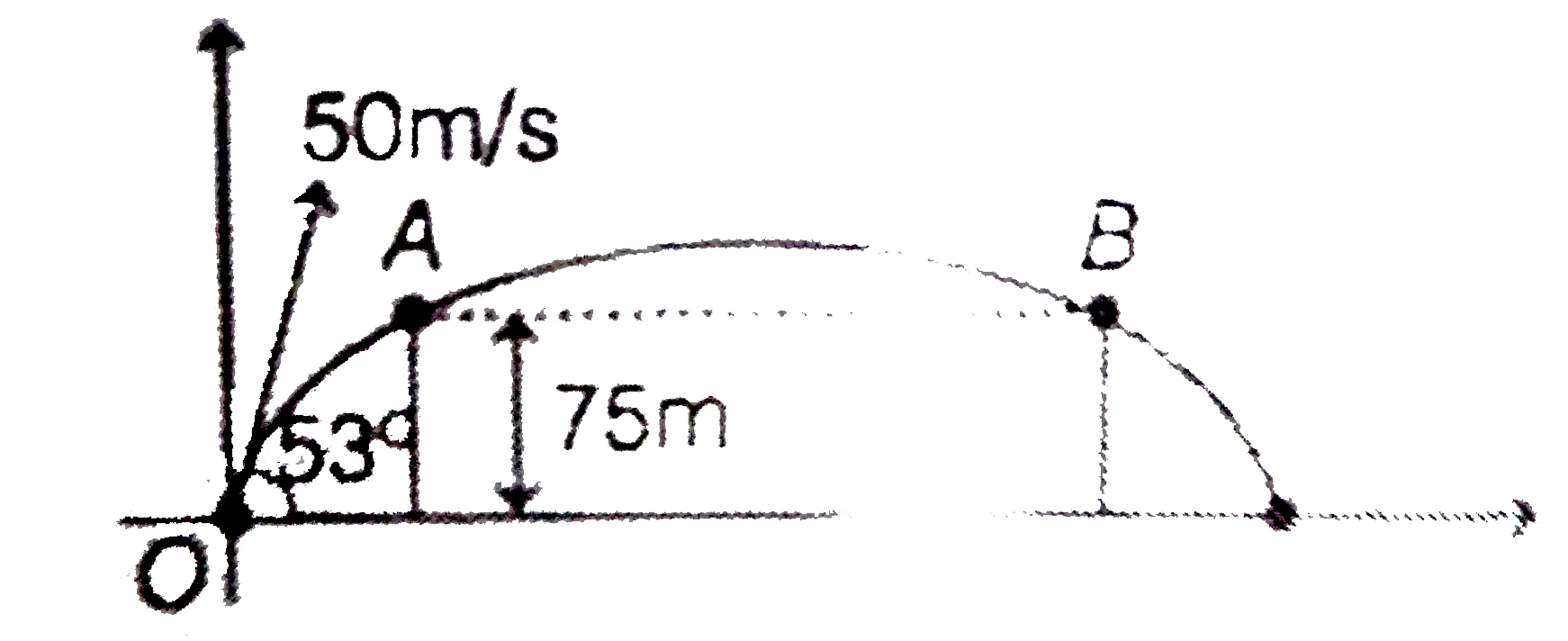
The horizontal separation between the points $A$ and $B$
A $30 m$
B $60 m$
C $90 m$
Dnone of these
A projectile is fired from the origin with a velocity $v_{0}$ at an angle $θ$ with x-axis. The speed of the projectile at an altitude $h$ is .
A $v_{0} cos θ$
B $\sqrt{v_{0}^{2} - 2 g h}$
C $\sqrt{v_{0}^{2} {sin}^{2} θ - 2 g h}$
DNone of these