If then
The correct Answer is:
To solve the question "If AB is congruent to CD, then...", we need to understand what congruence means in the context of geometry, particularly with triangles or line segments.
1. Understanding Congruence:
- Congruence in geometry means that two figures have the same shape and size. For line segments, this means they have the same length.
2. Given Information:
- We are given that line segment AB is congruent to line segment CD. This can be written as:
AB≅CD
3. Implication of Congruence:
- Since AB is congruent to CD, we can conclude that the lengths of these segments are equal. Therefore:
Length of AB=Length of CD
4. Conclusion:
- The statement "If AB is congruent to CD" implies that both segments are equal in length. Thus, we can state:
AB=CD
Final Answer:
If AB≅CD, then AB=CD.
---
- Congruence in geometry means that two figures have the same shape and size. For line segments, this means they have the same length.
- We are given that line segment AB is congruent to line segment CD. This can be written as:
AB≅CD
- Since AB is congruent to CD, we can conclude that the lengths of these segments are equal. Therefore:
Length of AB=Length of CD
- The statement "If AB is congruent to CD" implies that both segments are equal in length. Thus, we can state:
AB=CD
If AB≅CD, then AB=CD.
Topper's Solved these Questions
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (Fill in the blanks )
10 Videos
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (State which of the following statements are true and false )
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test
8 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium such that AB and CD are parallel and BC⊥CD if ∠ADB=θ,Bc=pandCD=q, then AB is equal to
A(p2+q2sinθpcosθ+qsinθB(p2+q2)cosθpcosθ+qsinthetCp2+q2p2cosθ+q2sinθD(p2+q2)sinθ(pcosθ+qsinθ)ABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
Ap2+q2cosθpcosθ+qsinθBp2+q2p2cosθ+q2sinθC(p2+q2)cosθ(pcosθ+qsinθ)2D(p2+q2)sinθpcosθ+qsinθABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
A((p2+q2))sinθpcosθ+qsinθBp2+q2cosθpcosθ+qsinθCp2+q2p2cosθ+q2sinθDq(p2+q2)(p2cosθ+q2sinθ)2
Two line segment AB and CD are congruent.
If AB = 6 cm, then what is the length of CD?
View SolutionIn the figure , If AB||CD then measure of p is
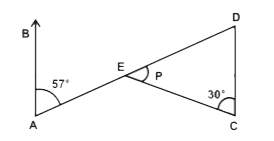
View SolutionIf AB∣∣CD then find y∘−x∘=
View SolutionIf △ABC≅△DEF then
AB = ________
View SolutionABCD is a trapezium such that ABandCD are parallel and BC⊥CD. If /_ADB= theta , BC =p and CD=q, then AB is equal to
View Solution
