ΔDEF is divided into two triangles ΔDEMandΔDFM of equal areas. Which of the following statement is true ?
ΔDEFandΔDFM have equal bases.
ar (ΔDEM)=13 ar (ΔDEF)
Mis the mid - point of side EF.
ΔDEMandΔDFM and congruent.
The correct Answer is:C
To solve the problem, we need to analyze the given information about triangle DEF, which is divided into two triangles, DEM and DFM, of equal areas. We will evaluate each option to determine which statements are true.
1. Understanding the Area of Triangles:
- The area of a triangle can be calculated using the formula:
Area=12×base×height
- Since triangles DEM and DFM have equal areas, we can express this mathematically:
Area of △DEM=Area of △DFM
2. Analyzing Option A:
- Option A states that triangles DEF and DFM have equal bases.
- If we denote the base of triangle DEM as EM and the base of triangle DFM as FM, we can set up the equation:
12×EM×h=12×FM×h
- Since the height (h) is the same for both triangles, we can cancel it out, leading to:
EM=FM
- This means that the bases of triangles DEM and DFM are equal. Therefore, Option A is true.
3. Analyzing Option B:
- Option B claims that the area of triangle DEM is equal to 13 of the area of triangle DEF.
- Since we know that the areas of triangles DEM and DFM are equal, we can express the area of triangle DEF as:
Area of △DEF=Area of △DEM+Area of △DFM=2×Area of △DEM
- Therefore, the area of triangle DEM is actually 12 of the area of triangle DEF, not 13. Thus, Option B is false.
4. Analyzing Option C:
- Option C states that M is the midpoint of side EF.
- Since we established that EM = FM, point M must indeed be the midpoint of side EF. Therefore, Option C is true.
5. Analyzing Option D:
- Option D claims that triangles DEM and DFM are congruent.
- To check for congruence, we can use the SSS (Side-Side-Side) criterion. We have:
- EM = FM (from Option A)
- DM is common to both triangles.
- However, we do not have information about the lengths DE and DF, so we cannot conclude that the triangles are congruent. Therefore, Option D is false.
Conclusion:
The true statements are:
- Option A: DEM and DFM have equal bases.
- Option C: M is the midpoint of side EF.
- The area of a triangle can be calculated using the formula:
Area=12×base×height
- Since triangles DEM and DFM have equal areas, we can express this mathematically:
Area of △DEM=Area of △DFM
- Option A states that triangles DEF and DFM have equal bases.
- If we denote the base of triangle DEM as EM and the base of triangle DFM as FM, we can set up the equation:
12×EM×h=12×FM×h
- Since the height (h) is the same for both triangles, we can cancel it out, leading to:
EM=FM
- This means that the bases of triangles DEM and DFM are equal. Therefore, Option A is true.
- Option B claims that the area of triangle DEM is equal to 13 of the area of triangle DEF.
- Since we know that the areas of triangles DEM and DFM are equal, we can express the area of triangle DEF as:
Area of △DEF=Area of △DEM+Area of △DFM=2×Area of △DEM
- Therefore, the area of triangle DEM is actually 12 of the area of triangle DEF, not 13. Thus, Option B is false.
- Option C states that M is the midpoint of side EF.
- Since we established that EM = FM, point M must indeed be the midpoint of side EF. Therefore, Option C is true.
- Option D claims that triangles DEM and DFM are congruent.
- To check for congruence, we can use the SSS (Side-Side-Side) criterion. We have:
- EM = FM (from Option A)
- DM is common to both triangles.
- However, we do not have information about the lengths DE and DF, so we cannot conclude that the triangles are congruent. Therefore, Option D is false.
The true statements are:
- Option A: DEM and DFM have equal bases.
- Option C: M is the midpoint of side EF.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)18videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, in ΔPQRandΔTQR,PQ=TRandPR=TQ. Which of the following statements is true?
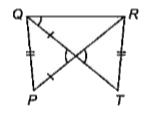 AΔPQR≅ΔRQTBΔPQR≅ΔQTRCΔPQR≅ΔTRQDΔPQR≅ΔTQR
AΔPQR≅ΔRQTBΔPQR≅ΔQTRCΔPQR≅ΔTRQDΔPQR≅ΔTQR - Question 2 - Select One
M, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
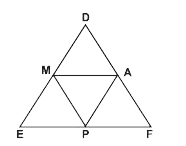 Aar (ΔMPF)=2 ar (ΔDEF)Bar (AMPF)=12 ar (ΔDEF)Car (ΔAMP)=14 ar (ΔDEF)Dar (AMPF)=12 ar (ΔDEF)
Aar (ΔMPF)=2 ar (ΔDEF)Bar (AMPF)=12 ar (ΔDEF)Car (ΔAMP)=14 ar (ΔDEF)Dar (AMPF)=12 ar (ΔDEF) - Question 3 - Select One
In ΔDEFandΔPQR, it is given that ∠D=∠Qand∠R=∠E, then which of the following is not true?
AEFPR=DFPQBDEPQ=EFRPCDEQR=DFPQDEFRP=DEQR
Median divides a triangle into two triangles of the same area
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Which of the following statements is/are correct?
1. The area of triangle ABC is equal to four times the area of triangle BED.
2. The area of triangle ADC is twice the area of triangle BED.
Select the correct answer using the code given below.View SolutionThree straight lines are drawn through the three vertices of a triangle ABC, the line through each vertex being parallel to the opposite side. The triangle DEF is bounded by these parallel lines. Consider the following statements in respect of the triangle DEF :
1. Each side of triangle DEF is double the side of triangle ABC to which it is parallel.
2. Area of triangle DEF is four times the area of triangle ABC.
Which of the above statements is/are correct?View SolutionIf ΔABC~ΔEDFandΔABC is not similar to ΔDEF then which of the following is not ture ?
View Solution

