In a rhombus ABCD, ∠ABC = 72∘. Find ∠ACD
The correct Answer is:Non-Collinear
To find the angle ACD in rhombus ABCD where angle ABC is given as 72°, we can follow these steps:
1. Understanding the Properties of a Rhombus:
In a rhombus, opposite angles are equal, and adjacent angles are supplementary (they add up to 180°).
2. Identify Given Information:
We know that angle ABC = 72°.
3. Determine Angle ADC:
Since opposite angles in a rhombus are equal, angle ADC is also 72°.
Angle ADC=Angle ABC=72°
4. Set Up the Triangle:
Consider triangle ACD. In this triangle, we know:
- Angle ADC = 72°
- Angles DAC and ACD are equal because AD = DC (sides of the rhombus).
Let’s denote angle DAC = angle ACD = y.
5. Use the Triangle Sum Property:
The sum of angles in triangle ACD is 180°. Therefore, we can write the equation:
Angle ADC+Angle DAC+Angle ACD=180°
Substituting the known values:
72°+y+y=180°
This simplifies to:
72°+2y=180°
6. Solve for y:
To isolate y, first subtract 72° from both sides:
2y=180°−72°
2y=108°
Now, divide both sides by 2:
y=108°2=54°
7. Conclusion:
Therefore, angle ACD is:
Angle ACD=54°
Final Answer:
Angle ACD = 54°.
In a rhombus, opposite angles are equal, and adjacent angles are supplementary (they add up to 180°).
We know that angle ABC = 72°.
Since opposite angles in a rhombus are equal, angle ADC is also 72°.
Consider triangle ACD. In this triangle, we know:
- Angle ADC = 72°
- Angles DAC and ACD are equal because AD = DC (sides of the rhombus).
The sum of angles in triangle ACD is 180°. Therefore, we can write the equation:
To isolate y, first subtract 72° from both sides:
Therefore, angle ACD is:
Angle ACD = 54°.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE QUESTION PAPER-2EXERCISE - PART D7videos
PRACTICE QUESTION PAPER-2
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE QUESTION PAPER-2EXERCISE - PART B8videos
PRACTICE QUESTION PAPER-2
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - POLYNOMIALSEXERCISE - Practice Test8videos
POLYNOMIALS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST QUESTION PAPER 1EXERCISE - SECTION-D5videos
PRACTICE TEST QUESTION PAPER 1
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a rhombus with ∠ABC=56∘, then ∠ACD is equal to:
 A90∘B60∘C56∘D62∘
A90∘B60∘C56∘D62∘ - Question 2 - Select One
If length of each side of a rhombus ABCD is 16 cm and ∠ABC=120∘ then what is the length ( in cm) of BD ?
A24B12C16D14√3 - Question 3 - Select One
In a rhombus ABCD, ∠ADC:∠BCD=1:2andEF:BD=1:3, where E and F lie on the diagonal BD, inside the rhombus, such that □AECF is a quadrlateral. Find the ratio of areas of □AECF:□ABCD.
AA. 1:4BB. 2:5Cc. 3:14DD. none of these
In the given figure ABCD is a rhombus with ∠ABC=56∘. Determine ∠ACD
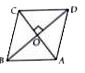 View Solution
View SolutionIn a rhombus, ABCD, ∠B=60∘, AB =14 cm. Find the diagonal AC.
View SolutionABCD is a rhombus. If ∠ACB=40∘, find ∠ADB.
View SolutionIn a rhombus ABCD, if ∠A=60∘ find ∠B,∠C&∠D.
View SolutionThe given figure shows a rhombus ABCD in which angle BCD=80∘. Find angles xandy.
View Solution

