If f:R→Randg:R→R are defined by f(x)=x5andg(x)=x4 then check if f, g are one-one and fog is one-one?Solution in Tamil
Step by step video & image solution for If f: R to R and g: R to R are defined by f(x)=x^(5) and g(x)=x^(4) then check if f, g are one-one and fog is one-one? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - EXERCISE 1.6
15 Videos
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - SOLUTION TO UNIT EXERCISE
14 Videos
- RELATIONS AND FUNCTION BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - EXERCISE 1.4
28 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
23 Videos
- STATISTICS AND PROBABILITY BOOK - PREMIERS PUBLISHERSCHAPTER - STATISTICS AND PROBABILITY EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
23 Videos
Similar Questions
If n(A×B)=6andA={1,3}, then n(B) is
View SolutionIf the ordered pairs (x2−3x,y2+4y)and(−2,5) are equal to then find x and y.
View SolutionDetermine whether the graph given below represents functions. Give reason for your answers concering each graph
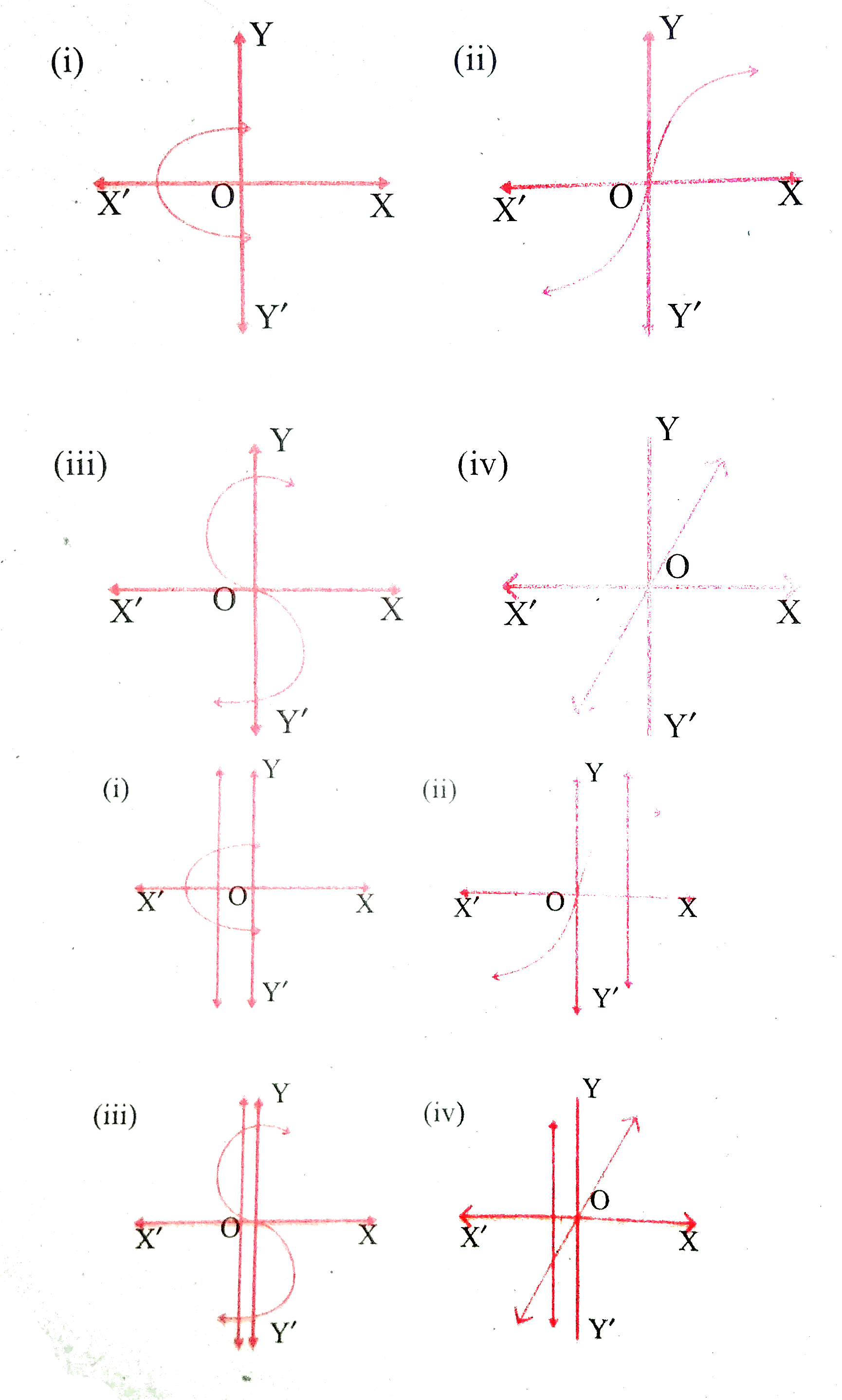
View SolutionThe quotient and remainder when 19 is divided by −3 are :
View SolutionIf the sum and mean of the data are 418 and 11 respectively then the no. of observation is the data is:
View SolutionFind gof and fog when f:R→R and g:R→R is defined by f(x)=x and g(x)=|x|
View SolutionLet f:R→R and g:R→R be defined by f(x)=x2 and g(x)=x+1 . Show that fog≠gof.
View SolutionIf f:R→R and g:R→R be functions defined by f(x)=x2+1 and g(x)=sinx, then find fog and gof .
View SolutionIf f:R→Randg:R→R are defined by f(x)=x5andg(x)=x4 then check if f, g are one-one and fog is one-one?
View SolutionFind fog and g o f when f : R → R and g : R → R is defined by f ( x ) = 5 x + x2 and g ( x ) = 2x
View Solutionयदि फलन f:R→R,f(x)=x2 तथा g:R→R,g(x)=sinx,x∈R से परिभाषित हो , तो (gof ) (x) और (fog)(x) ज्ञात कीजिए तथा सिद्ध कीजिए कि gof≠fog
View SolutionLet f:R→Tandg:R→R be the function defined by f(x)=x1+x2,x∈R,g(x)=x21+x2,x∈R
Then, the correct statement (s) among the following is/are:
(A) both f, g are one-one
(B) Both f, g are onto
(C ) both f, g are not one-one as well as not onto
(D) f and g onto but not one-one
View Solutionयदि f:R→R तथा g:R→R निम्न प्रकार परिभाषित हों कि f(x)=x2 तथा g(x)=√x तो (fog) ज्ञात कीजिए।
View Solutionf:R→R and g:[0,∞)→R is defined by f(x)=x2 and g(x)=√x. Which one of the following is not true?
View SolutionFind gof and fog when f:R→R and g:R→R is defined by f(x)=2x+3 and g(x)=x2+5
View SolutionFind gof and fog when f:R→R and g:R→R is defined by f(x)=2x+x2 and g(x)=x3
View Solution
