The first term of an arithmetic progressions is unity and the common difference is 4. Which of the following will be a term of this A.P.Solution in Tamil
4551
10091
7881
13531
The correct Answer is:C
Step by step video, text & image solution for The first term of an arithmetic progressions is unity and the common difference is 4. Which of the following will be a term of this A.P. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - UNIT EXERCISE12videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - THINKING CORNER13videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - EXERCISE 2. 914videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS16videos
MENSURATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS25videos
RELATIONS AND FUNCTION
Similar Questions
Prove that n2−n divisible by 2 for every positive integer n.
04:30View SolutionWhen a positive integer is divided by 3
What are the possible remainders?01:14View SolutionFind the sum of the following series
1+2+3+…+6006:01View SolutionMatch the following:
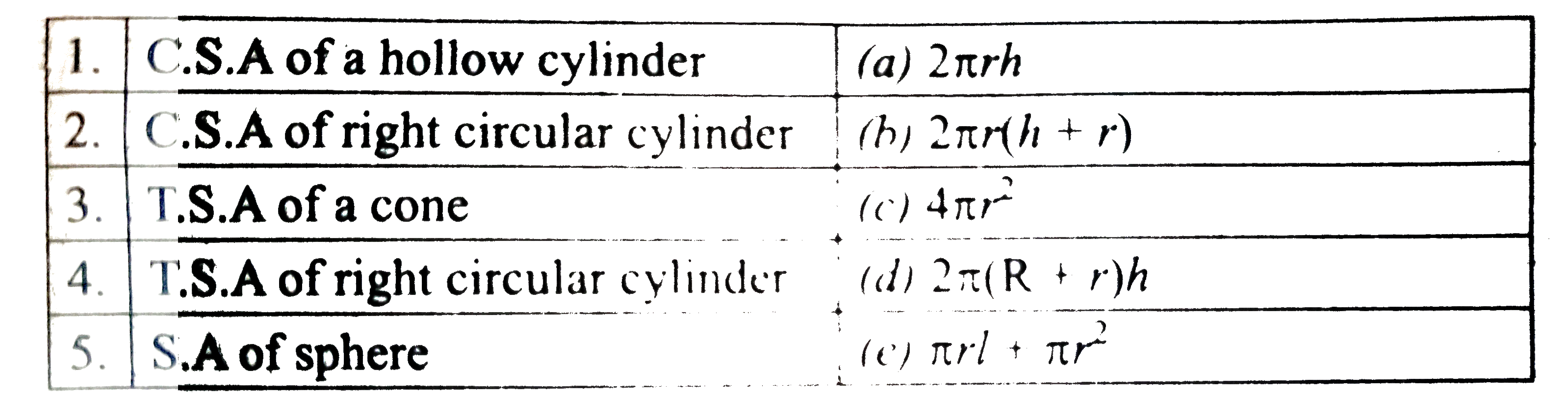 02:07View Solution
02:07View SolutionIf n(A×B)=24andA={1,3,5,7}then n (B) is
02:57View SolutionSuppose that all the terms of an arithmetic progression (A.P.) are natural numbers. If the ratio of the sum of the first seven terms to the sum of the first eleven terms is 6:11 and the seventh term lies in between 130 and 140, then the common difference of this A.P. is
05:13View SolutionThe sum of the first 20 terms of an arithmetic progression whose first term is 5 and common difference is 4, is __________.
02:41View SolutionThe sum of the fist ten terms of an A.P. , equals 155
and the sum of the first two terms of a G.P. equals
9. The first term of the A.P. is equal to the common
ratio of the G.P. and the common difference of the
A.P. is equal to the first term G.P.. Give that the
common difference of the A.P. is less then unity,
which of the following is correct ?02:46View SolutionFind the first term and common difference of the Arithmetic Progressions whose nth terms are given below
tn=4−7n04:27View SolutionThe first term of an arithmetic progressions is unity and the common difference is 4. Which of the following will be a term of this A.P.
04:16View SolutionThe first term of an arithmetic progression is uinty and the common difference is 4. Which of the following will be a term of this A.P..................... .
05:09View SolutionSuppose that all the terms of an arithmetic progression (A.P.) are natural numbers. If the ratio of the sum of the first seven terms to the sum of the first eleven terms is 6: 11 and the seventh term lies in between 130 and 140, then the common difference of this A.P. is
06:33View SolutionSuppose that all the terms of an arithmetic progression (A.P.) are natural numbers. If the ratio of the sum of the first seven terms to the sum of the first eleven terms is 6: 11 and the seventh term lies in between 130 and 140, then the common difference of this A.P. is
06:33View SolutionIn a arithmetic progression of 16 distinct terms with a1=16, the sum is equal to square of the last term. The common difference of the A.P. is
01:28View SolutionSuppose that all the terms of an arithmetic progression (A.P) are natural numbers. If the ratio of the sum of the first seven terms to the sum of the first eleven terms is 6 : 11 and the seventh terms lies in between 130 and 140, then the common difference of this A.P, is
02:26View SolutionThe sum of the first ten terms of an A.P. , equals 155
and the sum of the first two terms of a G.P. equals
9. The first term of the A.P. is equal to the common
ratio of the G.P. and the common difference of the
A.P. is equal to the first term G.P.. Give that the
common difference of the A.P. is less then unity,
which of the following is correct ?02:33View Solution

