माना की T, बिंदुओं P(−2,7) और Q(2,−5) से गुजरने वाली रेखा (line) है| माना की F1 उन सभी वृत्त युग्मों (pairs of circles) (S1,S2) का सम्मुच्य (set) है रेखा T, S1 के बिंदु P पर और S2 के बिंदु Q पर स्पर्शी (tangent) है तथा वृत्त S1 व S2 एक दूसरे को बिंदु माना की M, पर स्पर्श करते है| जब युग्म (S1,S2),F1 में विचरित (varies) करता है तो माना की सम्मुच्चय (set) E1 बिंदु M के बिन्दुपथ को दर्शाता है| माना की F2 उन सरल रेखा-खण्डों का सम्मुच्य है जो बिंदु R(1,1) से गुजरती है तथा E1 के दो भिन्न बिंदुओं के युग्म को जोड़ती है| माना की E2 सम्मुच्य F2 के रेखाख़ण्डों के मध्य बिंदुओं का सम्मुच्य है| तब निम्नलिखित में से कौन सा (से) कथन सत्य है?
बिंदु (−2,7) सम्मुच्य E1 में स्थित है|
बिंदु (45,75) सम्मुच्य E2 में स्थित नहीं है|
बिंदु (12,1) सम्मुच्य E2 में स्तिथ है
बिंदु (0,32) सम्मुच्य E1 में स्थित नहीं है|
The correct Answer is:A, D
Step by step video, text & image solution for माना की T, बिंदुओं P(-2,7) और Q(2,-5) से गुजरने वाली रेखा (line) है| माना की F_(1) उन सभी वृत्त युग्मों (pairs of circles) (S_(1),S_(2)) का सम्मुच्य (set) है रेखा T, S_(1) के बिंदु P पर और S_(2) के बिंदु Q पर स्पर्शी (tangent) है तथा वृत्त S_(1) व S_(2) एक दूसरे को बिंदु माना की M, पर स्पर्श करते है| जब युग्म (S_(1),S_(2)),F_(1) में विचरित (varies) करता है तो माना की सम्मुच्चय (set) E_(1) बिंदु M के बिन्दुपथ को दर्शाता है| माना की F_(2) उन सरल रेखा-खण्डों का सम्मुच्य है जो बिंदु R(1,1) से गुजरती है तथा E_(1) के दो भिन्न बिंदुओं के युग्म को जोड़ती है| माना की E_(2) सम्मुच्य F_(2) के रेखाख़ण्डों के मध्य बिंदुओं का सम्मुच्य है| तब निम्नलिखित में से कौन सा (से) कथन सत्य है? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED सोल्वड पेपर्स 2018 BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सोल्वड पेपर्स 2018 EXERCISE - पेपर 2 (खण्ड 2)
8 Videos
- JEE ADVANCED सोल्वड पेपर्स 2018 BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सोल्वड पेपर्स 2018 EXERCISE - पेपर 2 (खण्ड 3)
4 Videos
- JEE ADVANCED सोल्वड पेपर्स 2018 BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सोल्वड पेपर्स 2018 EXERCISE - (पेपर 1) खण्ड 3 (अनुछेद A)
2 Videos
- JEE ADVANCED सॉल्वड पेपर 2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर 2019EXERCISE - पेपर 2 खण्ड 3
4 Videos
- JEE MAIN 2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE MAIN 2019EXERCISE - 12 January Shift-II
30 Videos
Similar Questions
समाकलन ∫1/201+√3(((x+1)2)(1−x6))14dx का मान है
View Solutionमाना की E1={x∈R:x≠1औरxx−1>0} और E2={x∈E1sin−1(loge(xx−1)} एक वास्तविक संख्या (real number) है|
(यहाँ प्रतिलोम त्रिकोणमितीय फलां (inverse trignometric function) sin−1x,[−π2,π2] में मान धारण करता है|
माना की फलन: f:E1→R,f(x)=loge(xx−1) के द्वारा परिभाषित है
और फलन f:E2→R,g(x)=sin−1lloge(xx−1) के द्वारा परिभाषित है|

दिए हुए विकल्पों में से सही विकल्प है
View Solutionएक संगीत की कक्षा में पाँच छात्र S1,S2,S3,S4 और S5 है और उनके लिए बैठने के पाँच स्थान R1,R2,R3,R4 और R5 एक पंक्ति में व्यवस्थित हैं, जहाँ शुरूआत में स्थान Ri छात्र Si,i=1,2,3,4,5 को आवंटित किया जाता है। लेकिन परीक्षा के दिन पाँचों छात्रों को पाँच स्थान यादृच्छिक आवंटित किये जाते है
परीक्षा के दिन छात्र S1 को उसका पूर्व आवंटित स्थान R1 मिलने तथा शेष छात्रों में से किसी को भी उसका पूर्व आवंटित स्थान नहीं मिलने की प्रायिकता है
View Solutionमाना कि f(x)=sin(πcosx)तथाg(x)=cos(2πsinx) दो फलन हैं जो x>0 में परिभाषित हैं | निम्नलिखित समुच्चय जिनके अवयवों को बढ़ते हुए क्रम (आरोही) में लिखा गया है, इस प्रकार परिभाषित हैं |
X={x:f(x)=0},Y={x:f'(x)=0}
Z={x:g(x)=0},W={x:g'(x)=0}
सूची-I में X, Y, Z और W समुच्चय हैं | सूची-II में इन समुच्चयों के बारे में कुछ सूचनाएं हैं |
सूची −I सूची−II
(I)X (P)⊇{π2,3π6,4π,7π}
(II)Y (Q) समांतर श्रेणी
(III)Z (R) समांतर श्रेणी नहीं है
(IV) W(S)⊇{π6,7π6,13π6}(T)⊇{π3,2π3,π}(U)⊇{π6,3π6}
निम्न में से कौन सा एक मात्र संयोजन सही है
View Solutionयदि λ के उन सभी वास्तविक मानो, जिनके लिए बिन्दुओ (−λ2,1,1),(1,−λ2,1) तथा (1,1−λ2) से होकर जाने वाला एक समतल, बिन्दु (−1,−1,1) से भी होकर जाता है, का समुच्चय S है, तो S बराबर है
View SolutionLet T be the line passing through the points P(-2, 7) and Q(2, -5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1andS2 touch each other at a point , say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segment joining a pair of disntinct point of E1 and passing through the point R(1, 1) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then , which of the following statement (s) is (are) TRUE?
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionरेखा y=x+a√2 वृत्त को x2+y2=a2 बिंदु …………. पर स्पर्श करता है ।
View SolutionLet T be the line passing the points P(–2, 7) and Q(2,–5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1 and S2 touch each other at a point, say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segments joining a pair of distinct points of E1 and passing through the point R(1,1,) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then, which of the following statment(s) is (are) TRUE ?
View SolutionIf F1,F2,F3 be the feet of the perpendicular from the foci S1,S2 of an ellipse x2/5+y2/3=1 on the tangent at any point P on the ellipse then S1F1⋅S2F2=
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
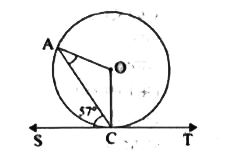
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solution
