Let T be the line passing through the points P(-2, 7) and Q(2, -5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1andS2 touch each other at a point , say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segment joining a pair of disntinct point of E1 and passing through the point R(1, 1) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then , which of the following statement (s) is (are) TRUE?
The point (-2, 7) lies in E1
The point (45,75) does NOT lie in E2
The point (12,1) lies in E2
The point (0,32)does NOT lie in E1
The correct Answer is:A, D
It is given that T is tangents to S1andS2 at Q and S1andS2 touch externally at M.
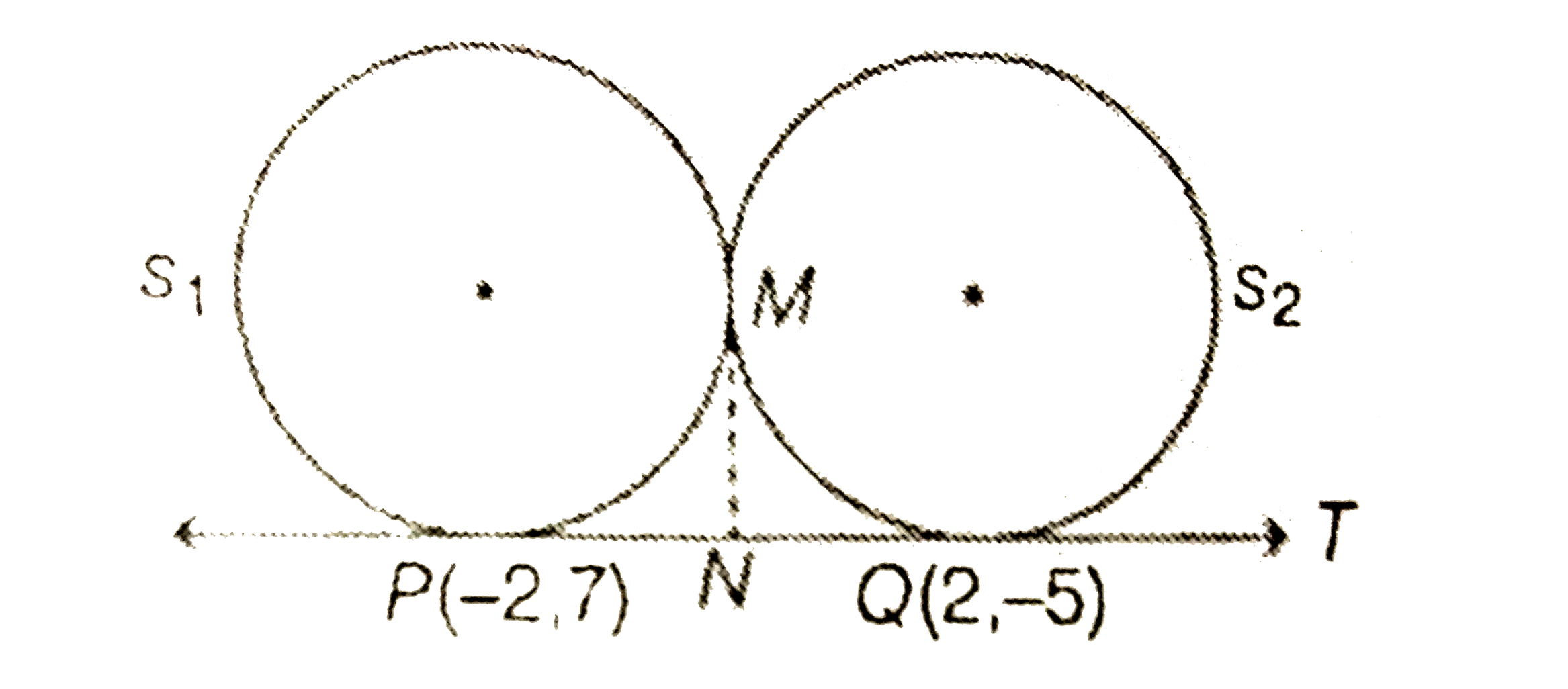
∴MN=NP=NQ
∴ Locus of M is a circle having PQ as its diameter of circle.
∴ Equation of circle
(x−2)(x+2)+(y+5)(y−7)=0
⇒x2+y2−2y−39=0
Hence, E1:x2+y2−2y−39=0,x≠±2
Locus of mid-point of chord (h,k) of the circle E_(1) is
xh+yk−(y+k)−39=h2+k2−2k−39
⇒xh+yk−y−k=h2+k2−2k
since, chord is passing through (1, 1). lt brgt ∴ Locus of mid-point of chord (h,k) is
h+k−1−k=h2+k2−2k
⇒h2+k2−2k−h+1=0
Locus is E2:x2+y2−x−2y+1=0
Now, after checking options, (a) and (d) are correct.
Topper's Solved these Questions
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 2 Passage Based Problems
3 Videos
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 2 Match the Columns
1 Video
- CIRCLEBOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 2 Relation between Two Circles
15 Videos
- BINOMIAL THEOREMBOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
8 Videos
- COMPLEX NUMBERSBOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
1 Video
Similar Questions
Let T be the line passing through the points P(−2, 7) and Q(2, −5) . Let F1 be the set of all pairs of circles (S1, S2) such that T is tangent to S1 at P and tangent to S2 at Q , and also such that S1 and S2 touch each other at a point, say, M . Let E1 be the set representing the locus of M as the pair (S1, S2) varies in F1 . Let the set of all straight lines segments joining a pair of distinct points of E1 and passing through the point R(1, 1) be F2 . Let E2 be the set of the mid-points of the line segments in the set F2 . Then, which of the following statement(s) is (are) TRUE? The point (−2, 7) lies in E1 (b) The point (45,75) does NOT lie in E2 (c) The point (12, 1) lies in E2 (d) The point (0,32) does NOT lie in E1
View SolutionLet T be the line passing through the points P(−2,7) and Q(2,−5) . Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q , and also such that S1 and S2 touch each other at a point, say, M . Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1 . Let the set of all straight lines segments joining a pair of distinct points of E1 and passing through the point R(1,1) be F2 . Let E2 be the set of the mid-points of the line segments in the set F2 . Then, which of the following statement(s) is (are) TRUE? The point (−2,7) lies in E1 (b) The point (45,75) does NOT lie in E2 (c) The point (12,1) lies in E2 (d) The point (0,32) does NOT lie in E1
View Solution
Knowledge Check
Let T be the line passing the points P(–2, 7) and Q(2,–5). Let F1 be the set of all pairs of circles (S1,S2) such that T is tangent to S1 at P and tangent to S2 at Q, and also such that S1 and S2 touch each other at a point, say M. Let E1 be the set representing the locus of M as the pair (S1,S2) varies in F1. Let the set of all straight line segments joining a pair of distinct points of E1 and passing through the point R(1,1,) be F2. Let E2 be the set of the mid-points of the line segments in the set F2. Then, which of the following statment(s) is (are) TRUE ?
AThe point (–2,7) lies in E1BThe point (45,75) does NOT lie in E2CThe point (12,1) lies in E2DThe point (0,32) does NOT lie in E1If S is the set of all straight lines and relation R is defined on S as T={(S1,S2):S1 is perpendicular to S2} then R is
Asymmetric onlyBreflexive and symmetric onlyCtransitive onlyDnone of theseLet E1E2andF1F2 be the chords of S passing through the point P∘ (1, 1) and parallel to the X-axis and the Y-axis, respectively. Let G1G2 be the chord of S passing through P∘ and having slope -1. Let the tangents to S at E1andE2 met at F3, and the tangents to S at G1andG2 meet at G3. Then , the points E3,F3andG3 lie on the curve
Let S be the circle in the XY-plane defined by the equation
x2+y2=4Ax + y = 4B(x−4)2+(y−4)2=16C(x−4)+(y−4)=4Dxy = 4
Let P be a variable point on the ellipse with foci S1 and S2 . If A be the area of △PS1S2 then find the maximum value of A
View SolutionConsider a family of circles passing through two fixed points A=(2,6)andB=(4,5). Also S1 is the circle having centre (1,2) and radius equal to 3. The angle between the pair of tangent drawn from the point (4,5) to the circle S1 is
View SolutionLet S1andS2 be circle passing through (2,3) and touching the coordinate acea and S be the circle having common points of S1andS2 as the centre and radius equal to G.M of radius of S1andS2 then
View SolutionLet S1andS2 be circle passing through (2, 3) and touching the coordinate axis and S be the circle having common points of S1andS2 as the centre and radius equal to G.M of radius of S1andS2 then
View SolutionThe graph of function f contains the point P(1,2)andQ(s,r). The equation of the secant line through P and Q is y=(s2+2s−3s−1)x−1−s. The value of f'(1), is
View Solution
