A continuous random varibale X has probability density function f(x)=kx20≤x<1 find k (X>6) Solution in Tamil
Step by step video & image solution for A continuous random varibale X has probability density function f(x)=kx^(2) 0 le x lt 1 find k (X gt6) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONSBOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.1
5 Videos
- PROBABILITY DISTRIBUTIONSBOOK - PREMIERS PUBLISHERSCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.2
18 Videos
- ORDINARY DIFFERENTIAL EQUATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - ORDINARY DIFFERENTIAL EQUATIONS EXERCISE - PROBLEMS FOR PRACTICE (ANSWER THE FOLLOWING QUESTIONS )
22 Videos
- THEORY OF EQUATIONSBOOK - PREMIERS PUBLISHERSCHAPTER - THEORY OF EQUATIONSEXERCISE - Problems for practice (Answer the following)
21 Videos
Similar Questions
Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its inverse images.
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionFind the order and degree of the following differential equation
y''=(2+y')34
View SolutionIf α and β are the roots of 2x2−5x+3=0 form the equation whose roots are α2 and β2
View SolutionX is continuous random variable with probability density function f(x)=x28,0≤x≤1. Then, the value of P(0.2≤X≤0.5) is
View SolutionIf f(x)= kx, 0 lt x lt 2 = 0 otherwise, is a probability density function of a random variable X , then find (i) value of k, (ii) P(1 lt x lt2).
View SolutionIf the p.d.f of a continuous random variable X is
f(x)=kx2(1−x),0<x<1
= 0 otherwise
Then the value of k is
View SolutionIf f(x)=⎧⎨⎩√1+kx−√1−kxxif−1≤x<02x+kx−1if0≤x≤1
is continuous at x = 0, then the value of k is
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.2≤X<0.6)
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(1.2≤X<1.8)
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.5≤X<1.5)
View SolutionIf X is the random variable with probability density function f(x) is given by
f(x)=⎧⎪⎨⎪⎩x+1−1≤x<0−x+10≤x<10otherwise
then find (i) the distribution function F(x) (ii) P(−0.5≤X≤0.5)
View SolutionIf f(x)={√1+kx−√1−kxxfor−1≤x02x2+3x−2for0≤x≤1 is continuous at x = 0 then find k.
View SolutionIf f(x) = {:{((sqrt(1+ + kx ) - sqrt(1-kx))/x , " for" -1 le x lt 0) , ( 2x^(2) + 3x -2, " for " 0 le x le 1):}
continuous at x = 0 , then k is equal to
View SolutionIf the p.m (probability mass function ) f(x) of a random varibale X is
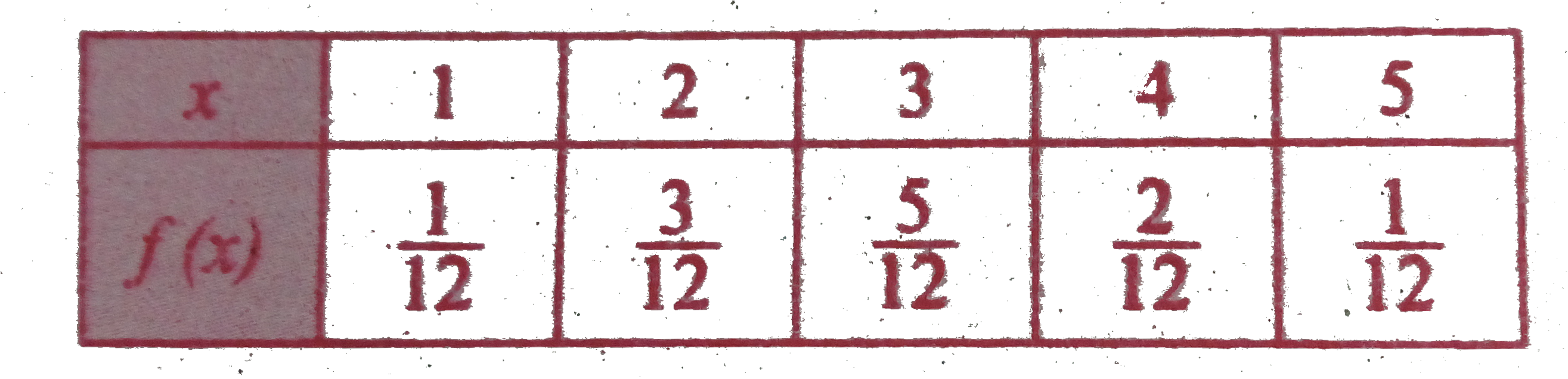 Find
Find
P(X≤3)
View Solution
