Question

A projectile is fired horizontally with a velocity u . Show that its trajectory is a parabola. Also obtain the expression for Time of flight .

Explanation

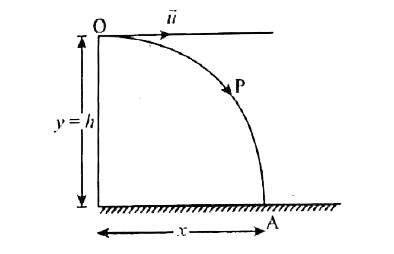
Let us consider a projectile, that is, thrown horizontal with an initial velocity `vec(u)` from the top of a tower of height h in the figure .
Motion along horizontal direction : The particle has zero acceleration along x direction. So, the initial velocity `u(x)` remains constant throughout the motion. The distance traveled by the projectile at a time t is given by `x = u_(x) t + (1)/(2) at^(2)`
Since a = 0 along x direction, we get
`x =u_(x)t " ". . . (1)`
Motion along downward direction : Here `u_(y) = 0 ` (initial velocity has no downward component), a = g .The distance y at time y is given by
`y = u_(y) t + (1)/(2) at ^(2)` , we get
`y = (1)/(2) g t^(2) ` [u = 0, a = g] . . . (2)
Substituting the value of t from equation (1) in equation (2) we have
`y = (1)/(2) g""(x^(2))/(u_(x)^(2))= ((g)/(2u_(x)^(2)))x^(2)`
`y = Kx^(2) " " . . . (3)`
Where `K = (g)/(2u_(x)^(2))` is a constant of proportionality .
Equation (3) gives the trajectory of the projectile. Thus , the path followed by the projectile is a parabola .
Time of Flight : The time taken for the projectile to complete its trajectory . It is also time taken by the projectile to hit the ground .
Consider a tower and a projectile . Let h be the height of a tower . Let T be the time taken by the projectile to hit the ground, after being thrown horizontally from the tower .
We know that `s_(y) =u_(y) t + (1)/(2) at ^(2)` for vertical motion . Here `s_(y) = h, t = T` (since there is no initial vertical velocity `u _(y) = 0`
`:. h = (1)/(2) g T^(2) (or) T = sqrt((2h)/(g))`