A projectile is fired horizontally with a velocity u . Show that its trajectory is a parabola. Also obtain the expression for .
Horizontal range .Solution in Tamil
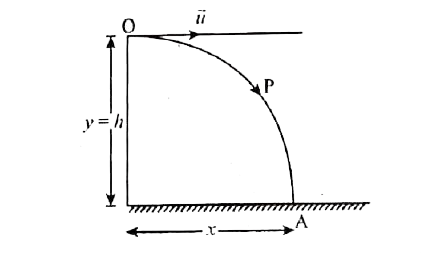
Let us consider a projectile, that is, thrown horizontal with an initial velocity →u from the top of a tower of height h in the figure .
Motion along horizontal direction : The particle has zero acceleration along x direction. So, the initial velocity u(x) remains constant throughout the motion. The distance traveled by the projectile at a time t is given by x=uxt+12at2
Since a = 0 along x direction, we get
x=uxt ...(1)
Motion along downward direction : Here uy=0 (initial velocity has no downward component), a = g .The distance y at time y is given by
y=uyt+12at2 , we get
y=12gt2 [u = 0, a = g] . . . (2)
Substituting the value of t from equation (1) in equation (2) we have
y=12gx2u2x=(g2u2x)x2
y=Kx2 ...(3)
Where K=g2u2x is a constant of proportionality .
Equation (3) gives the trajectory of the projectile. Thus , the path followed by the projectile is a parabola .
Horizontal range : The horizontal distance covered by the projectile from the foot of the tower to the point where the projectile hits the ground is called horizontal range. For horizontal motion, we have
sx=uxt+12at2
Here, sx=R (range), ux=u,a=0 (no horizontal acceleration) T is time of flight . Then horizontal range = u T.
Since the time of flight T =√2hg , we substitute this and we get the horizontal range of the particle as R=u√2hg .
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (V. Numerical problems).166videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (III. Short answer questions).26videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (CONCEPTUAL QUESTIONS)34videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)8videos
KINETIC THEORY OF GASES
Similar Questions
A crow is sitting on a branch of tree whose co-ordinates are (1,2,3) . A hunter is standing on the ground . Represent the position of the crow with respect to the hunter .
02:15View SolutionWrite note on function with example.
03:39View SolutionWhy a body weighs less at the equator than at the poles?
03:43View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
05:10View SolutionIn case of a projectile fired at an angle equally inclined to the horizontal and vertical with velocity (u). The horizontal range is:-
03:01View SolutionThe trajectory of a projectile fired horizontally with velocity u is parabola given by-
07:08View SolutionA projectile is fired horizontally with a velocity u. obtain the expression for resultant velocity of the projectile at any instant .
09:47View SolutionA projectile is fired horizontally with a velocity u . Show that its trajectory is a parabola. Also obtain the expression for Time of flight .
03:01View SolutionA projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight .
04:21View SolutionWhat is a projectile ? Obtain an expression for: maximum height , time of flight and the horizontal range when a projectile is fired at an angle theta with the horizontal.
03:08View SolutionA projectile is fired at an angle θ with horizontal. (a) Show that its trajectory is a parabola (b) Prove that for a given velocity of projection the horizontal range is same for (90∘−θ) (c) Obtain an expression for velocity of projectile at any instant.
03:19View SolutionA projectile is fired with a velocity u in such a way that its horizontal range is three times the maximum height aatained . Find the value of horizontal range .
08:49View SolutionA projectile is fired with a velocity 'u' making an angle theta with the horizontal. Show that its trajectory is a parabola.
07:33View SolutionObtain an expression for Horizontal Range of a projectile.
01:17View SolutionThe trajectory of a projectile fired horizontally with velocity u is a parabola given by
View Solution

