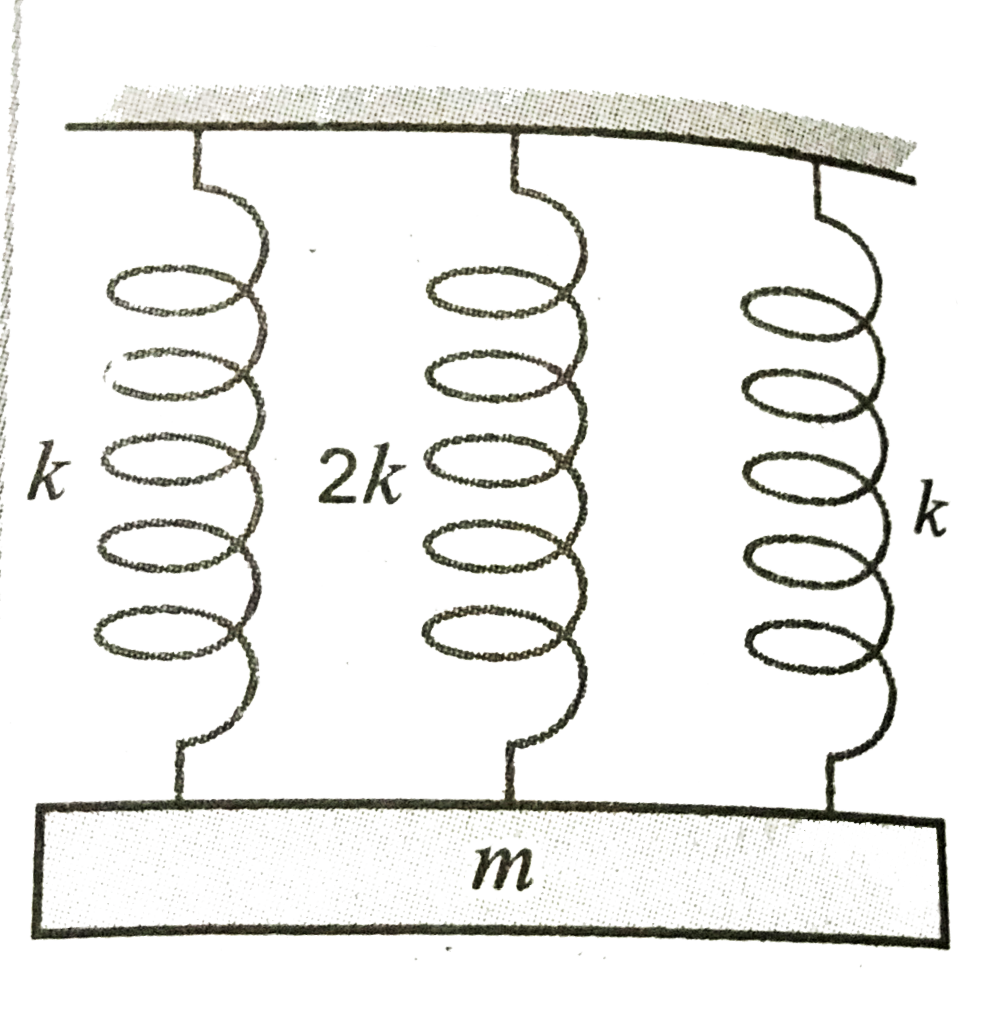
Three springs are connected to a mass as shown in figure (a). When mass oscillates, what is the effective spring constant and time period of vibration ? Given k=2Nm−1andm=80gm.

The equivalent arrangement of spring system is shown in figure. (b). This shows that all the springs are connected in parallel.
∴ effective spring constant.
k=k+2k+k=4k
k=4×2=8Nm−1
m=80×10−3kg=0.08kg
Time period
T=2π√m/4k=2×227√0.08/8
=0.628s
Topper's Solved these Questions
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( CONCEPTUAL QUESTIONS.)
24 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( LONG ANSWER QUESTIONS )
12 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
- PROPERTIES OF MATTERBOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (NUMERICAL PROBLEMS)
56 Videos
Similar Questions
Three springs are connected to a mass m as shown in figure, When mass oscillates, what is the effective spring constant and time period of vibration? Given k=2Nm−1 and m=80 gram.
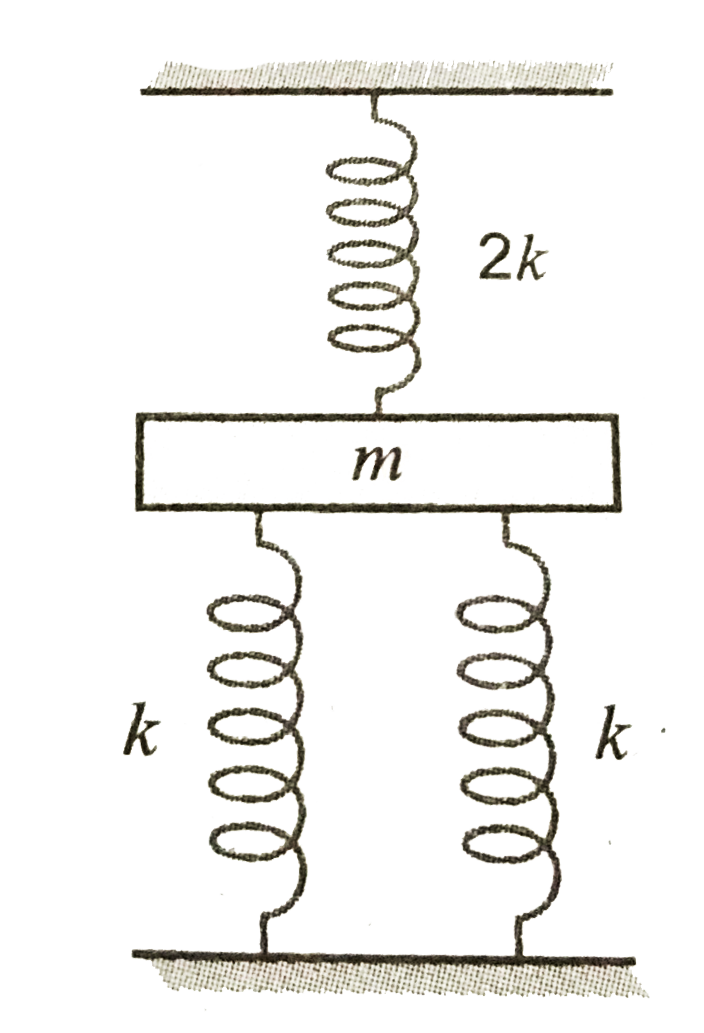
View SolutionThree spring are connected to a mass m(=100g) as shown in figure. Given k=2.5Nm−1. (a) What is the effecitve spring constant of the combination of spring constant of the combination of springs? (b) When mass m oscillates, find time period of its vibration.
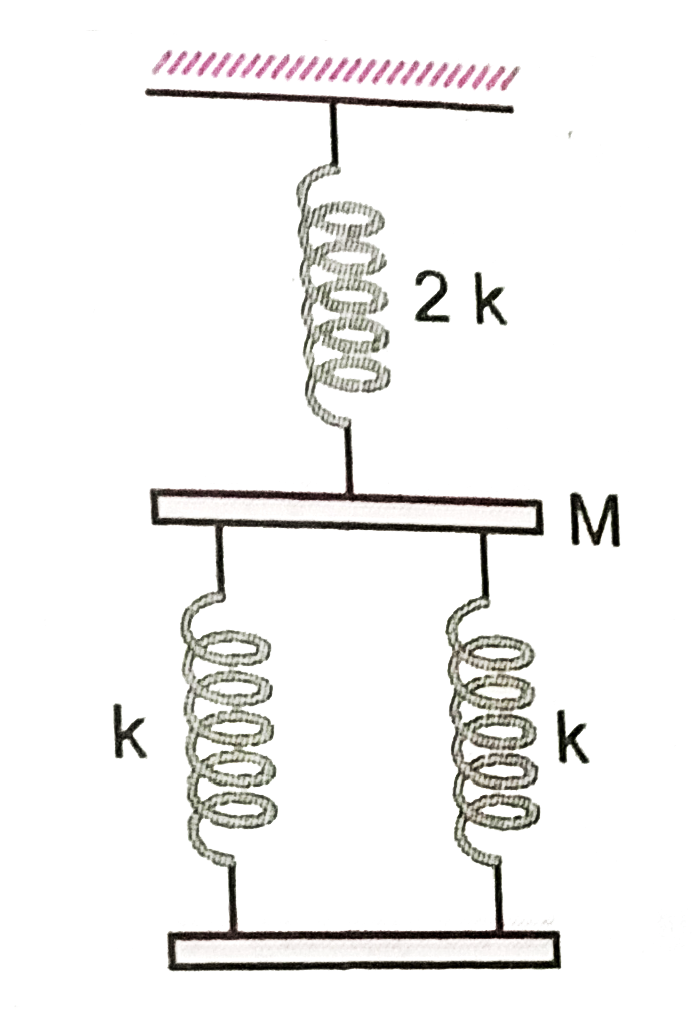
View Solution
Knowledge Check
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
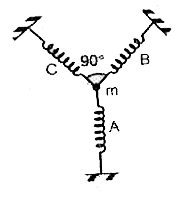 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
The figure shows the arrangement of three springs of different spring constant, connected to a mass m. When mass m oscillates find equivalent spring constant and the time period of vibration.
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionThe two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be

View SolutionThe two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
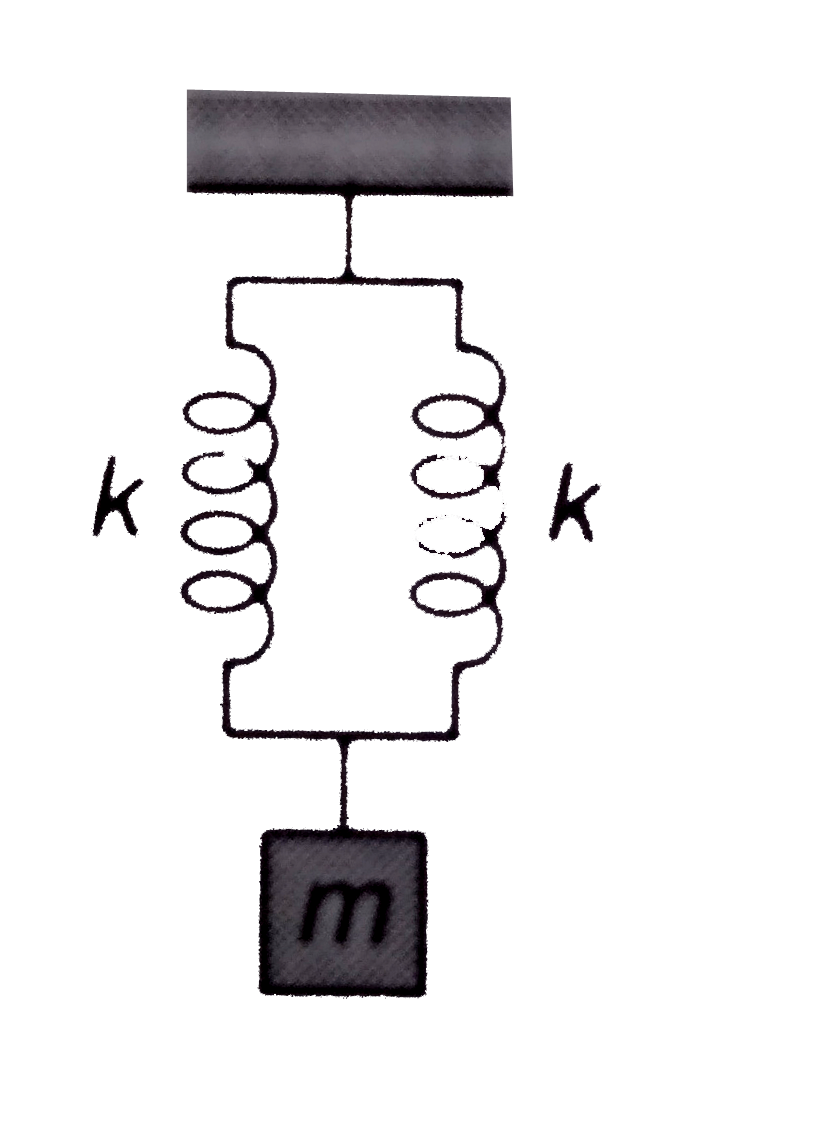
View SolutionTwo springs are joined and connected to mass m as shown. If the springs separately have force constants K1 and K2 , then frequency of oscillation of mass m is

View Solution
