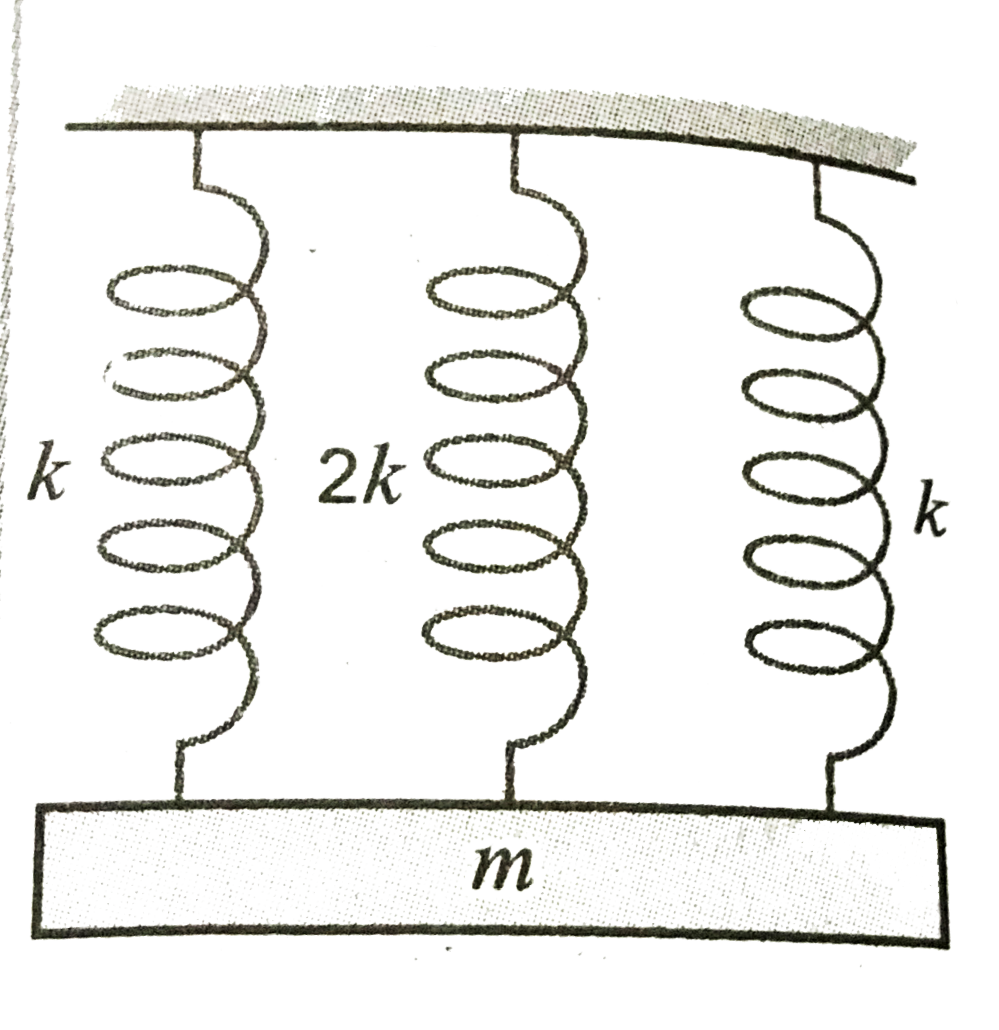
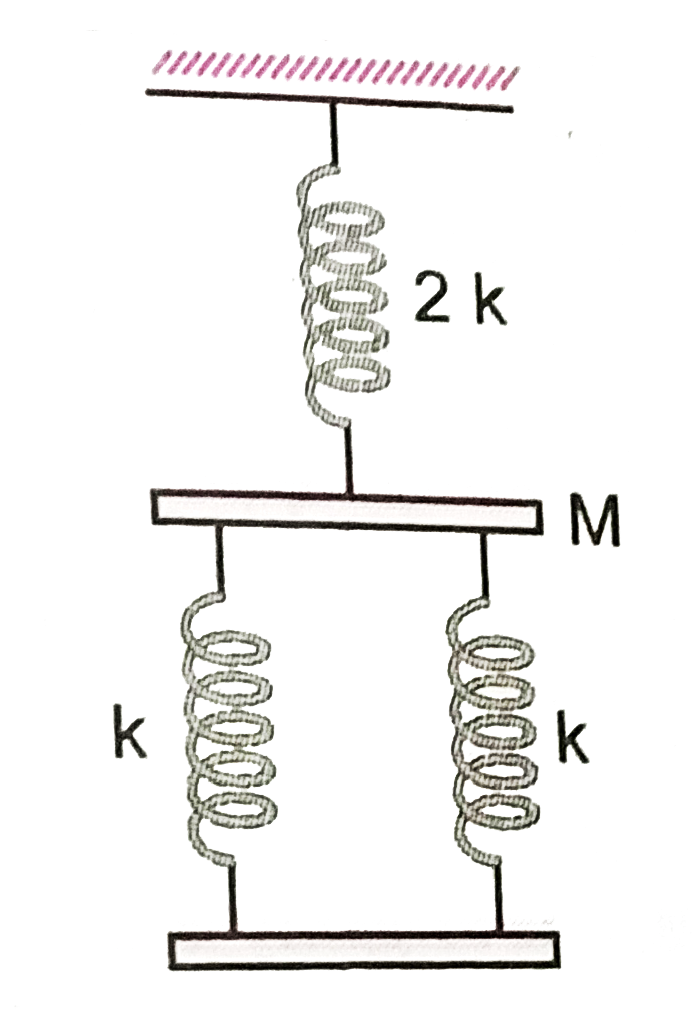
The figure shows the arrangement of three springs of different spring constant, connected to a mass m. When mass m oscillates find equivalent spring constant and the time period of vibration.
In lower part, there are two springs of force constant 2k and k, connected in parallel. So, their effective spring constant is
∴kp=2k+k=3k
The arrangment is now simplified as show in figure.
Now we have two spring (each of force constant 3k) connected in series.
∴ Effective spring constant of the system is
ks=k1k2k1+k2=3k×3k3k+3k=9k36k=32k
The time period is
T=2π√mks=2π√2m3k.

Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Very Short Answer Questions)
37 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Additional Question )
3 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question ( short Answer Type Questions )
6 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Three springs are connected to a mass m as shown in figure, When mass oscillates, what is the effective spring constant and time period of vibration? Given k=2Nm−1 and m=80 gram.
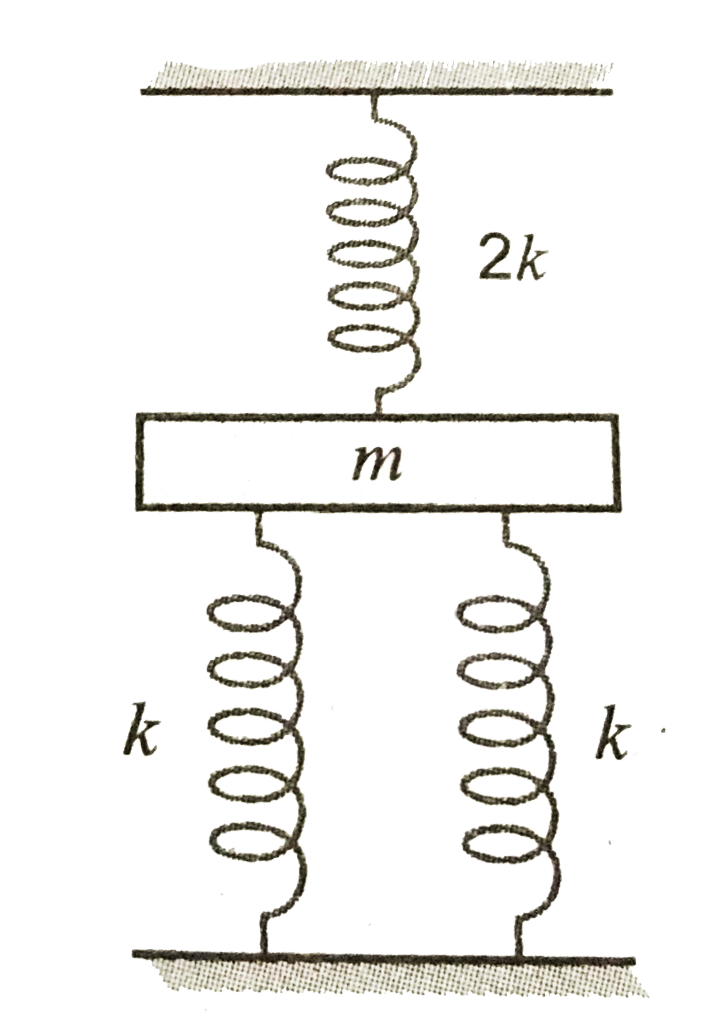
View SolutionThe figure shows an arrangement of mass m with three springs of different springs constant. When m is slightly displaced and then released, find the frequency of its motion.
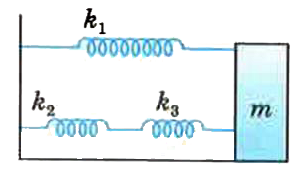
View Solution
Knowledge Check
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
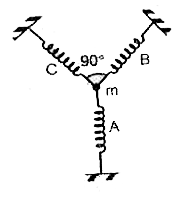 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)Two masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
AT=2π√1k(m1m2m1+m2)BT=2π√1k(m1+m2m1m2)CT=2π√(m1k)DT=2π√(m2k)
Find the equivalent spring constant for the following arrangements:
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionThree spring are connected to a mass m(=100g) as shown in figure. Given k=2.5Nm−1. (a) What is the effecitve spring constant of the combination of spring constant of the combination of springs? (b) When mass m oscillates, find time period of its vibration.
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution
