Question

Explain in detail the triangle law of addition.

Explanation

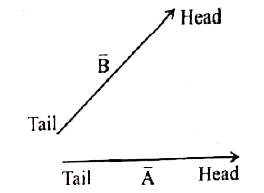
Let consider two vectors `vec(A) and vec(B)` as shown in figure.
Let us find the resultant of the two vectors apply the triangular law of addition as follows :
The vectors `vec(A) and (B)` are represented by the two adjacent sides of a triangle taken in the same order . Given the resultant the third side of the triangle. It is shown in figure.
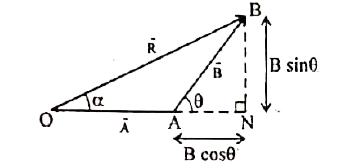
The head of hte first vector `vec(A)` is connected to the tail of the second vector `vec(B)` . Let the angle between `vec(A) and vec(B) "be" theta . "Then "vec(R)` is the first vector `vec(A)` to the head of the second vector `vec(B)` . The magnitude of `vec(R)` (resultant) is given geometrically by the length of `vec(R)` (OQ) . The direction of the resultant vector is given by the angle between `vec(R) and vec(A)` . Hence, `vec(R) = vec(A) + vec(B)` .
`vec(OQ) = vec(OP)+vec(PQ)`
(i) Magnitude of resultant vector : The magnitude and direction of the resultant vector are detemined from the following derivatives .
From the figure let us consider teh triangle ABN, that is obtained by extending the side OA to ON . ABN is a right angled triangle
From the figure .
`cos theta = (AN)/(B) :. AN = B cos theta and`
`sin theta = (BN)/(B) :. BN =B sin theta`
For `Delta OBN`, we have
`OB^(2) = ON^(2) +BN^(2)`
`:. R^(2) = (A +B cos theta)^(2) + (B sin theta)^(2)`
`rArr R^(2) = A^(2) + B^(2) cos ^(2) theta + 2AB cos theta + B^(2) sin ^(2) theta`
`rArr R^(2) = A^(2) + B^(2) (cos^(2) theta + sin ^(2) theta) + 2AB cos theta`
`:. R = sqrt(A^(2) + B^(2) + 2AB cos theta)`
That the magnitude of the resultant of `vec(A) and vec(B)`
(ii) Direction of resultant vectors : If `theta` is the angle between `vec(A) and vec(B)`
If `vec(R) ` makes an angle `alpha` with `vec(A)` , then in `Delta OBN`
`tan alpha = (BN)/(ON) = (BN)/(OA +AN)`
`rArr (B sin theta)/(A + B cos theta)`
`:.` Its direction is given by
`alpha = tan^(-1) ((B sin theta)/(A + B cos theta))`