Discuss the properties of scalar and vector Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Properties of scalar product are :
(i) The product quantity $\to A, \to B$ is always a sxalar. It is positive if the angle between the vectors is acule (i.e., $θ < 90^{\circ}$ . It is negative if the angle between them is obtuse (i.e., $90^{\circ} < θ < 180^{\circ}$ )
(ii) The scalar product obeys commutative law i.e., $\to A . \to B = \to B . \to A$
(iii) The vectors obeys distributive law i.e., $\to A . (\to B + \to C) = \to A . \to B + \to A . \to C$
(iv) The angle between the vectors ,
$θ = {cos}^{- 1} [\frac{\to A . \to B}{A B}]$
(v) The scalar product of two vectors will be maximum when $cos θ = 1, i . e . θ = 0^{\circ}, so {(\to A . \to B)}_{max} = A B$
(vi) The scalar product of two vectors will be minimum, when $cos θ = - 1, i . e ., θ = 180^{\circ}$ . When the vectors are anti-parallel.
${(\to A . \to B)}_{min} = - A B$
(vii) If two vectors $\to A and \to B$ are perpendicular to each other then their scalar product $\to A . \to B = 0$ , because ${cos 90}^{\circ} = 0$ . Then the vectors $\to A and \to B$ are said to be mutually orthogonal .
(viii) The scalar product of a vector with itself is termed as self-dot product. It is given by ${(\to A)}^{2} = \to A . \to A = A A cos θ = A^{2}$ . Here angle $θ = 0^{\circ}$
The magnitude of the vector is given by $\to A i s ∣ ∣ \to A ∣ ∣ = A = \sqrt{A} . \to A$
(ix) In case of a unit vector , $ˆ n$
$ˆ n . ˆ n = 1 \times 1 \times cos 0 = 1$ . For example, $ˆ i . ˆ i = ˆ j . ˆ j = ˆ k . ˆ k =$
(x) In the case of orthogonal unit vectors $ˆ i . ˆ j and h t a (k)$ ,
$ˆ i . ˆ j = ˆ j . ˆ k = ˆ k . ˆ i = 1.1 {cos 90}^{\circ} = 0$
(xi) In terms of components the scalar product of $\to A and \to B$ can be written as
$\to A . \to B = (A, ˆ i + A ˆ j + A, ˆ k) . (B, ˆ i + B, ˆ j + B, ˆ k)$
$= A_{x} B_{x} + A_{y} B_{y} + A_{z} B_{z}$ , With all other terms zero.
The magnitude of vector $∣ ∣ \to A ∣ ∣$ is given by
$∣ ∣ \to A ∣ ∣ = A = \sqrt{A_{x}^{z} + A_{y}^{2} + A_{z}^{2}}$
Properties of vector (cross) product are :
(i) The vector product of any two vectors is always another vector whose direction is perpendicular to the piane containing these two vectors , i.e., orthogonal to both the vectors $\to A and \to B$ . In this case. the vectors $\to a and \to B$ may or may not be mutually othogonal .
(ii) The vector of two vectors is not commutative, i.e., $\to A \times \to B \neq \to B \times \to A$ But ., $\to A \times \to B = - [\to B \times \to A]$ .
But , $∣ ∣ \to A \times \to B ∣ ∣ = ∣ ∣ \to B \times \to A ∣ ∣ = A B sin θ i . e .,$ in the case of the product vectors $\to A \times \to B and \to B \times \to A$ , the magnitudes are equal but directions are opposite to each other .
(iii) The vector product of two vectors will have maximum magnitude when sin $θ = 1, i . e ., θ = 90^{\circ}$ i.e., when the vectors $\to A and \to B$ are orthogonal to each other .
${(\to A \times \to B)}_{max} = A B ˆ n$
(iv) The vector product of two non-zero vectors will be minimum when $| sin θ | = 0, i . e ., θ = 0^{\circ} or 180^{\circ}$
${(\to A \times \to B)}_{min} = 0$
If the vectors are either parallel or anti parallel i.e., then the vector product of two non-zero vectors vanishes.
(v) The self - cross product, i.e., product of a vector with itself is the null vector
$\to A \times \to A = A A {sin 0}^{\circ} ˆ n = \to 0$
The null vector $\to 0$ is simple denoted as zero in physics.
(vi) The self-vector products of unit vectors are thus zero .
$ˆ i \times ˆ i = ˆ j \times ˆ j = ˆ k \times ˆ k = \to 0$
(vii) In the case of orthogonal unit vectors, $ˆ i, ˆ j, ˆ k$ in accordance with the right hand screw rule
$ˆ i \times ˆ j = ˆ k, ˆ j \times ˆ k = ˆ i and ˆ k \times ˆ i = ˆ j$
Also, since the cross product is not commutative,
$ˆ j \times ˆ i = - ˆ k, ˆ k \times ˆ j = - ˆ i and ˆ i \times ˆ k = - ˆ j$
(viii) In terms of components the vector product of two vectors $\to A and \to B$ is $\to A \times \to B = ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k A_{x} & A_{y} & A_{z} B_{x} & B_{y} & B_{z} \end{matrix} ∣ ∣ ∣ ∣ ∣$
$⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \begin{matrix} ˆ i (A_{y} B_{z} - A_{z} B_{y}) + ˆ j (A_{z} B_{x} - A_{x} B_{z}) + ˆ k (A_{x} B_{y} - A_{y} B_{x}) \end{matrix}$
Note that in the ${ˆ j}^{t h}$ component the order of multiplication is different than ${ˆ i}^{t h} and {ˆ k}^{t h}$ components .
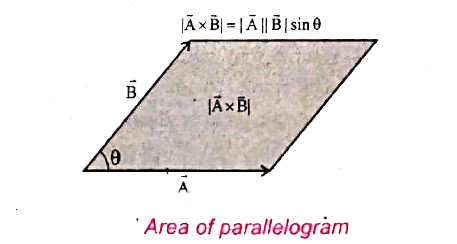
(ix) If two vectors $\to A and \to B$ form adjacent sides in a parallelogram, then the magnitude of $∣ ∣ \to A \times \to B ∣ ∣$ will give the area of the parallelogram as represented graphically in the figure.
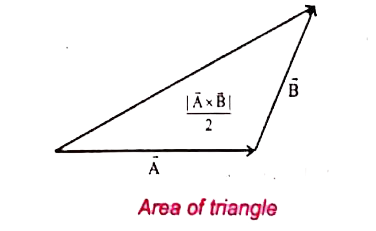
(x) Since a parallelogram is divided into two equal triangles as shown in the figure, the area of a triangle with $\to A and \to B$ as sides is $\frac{1}{2} ∣ ∣ \to A \times \to B ∣ ∣$ .

Updated on:21/07/2023

|

Class 11 PHYSICS MOTION IN A STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

PREMIERS PUBLISHERS-KINEMATICS -Textbook questions & answers (III. Long answer questions).

Home
Ask Doubt
Profile