How can the phase difference of two particles executing simple harmonic motions ?Solution in Tamil
Consider two particles executing simple harmonic motions. Their equations for displacement are
Y1=Asin(ωt+ϕ1)andY2=Asin(ωt+ϕ2) then the phase difference is given by Δϕ
Δϕ=(ωt+ϕ2)−(ωt+ϕ1)
=ϕ2=ϕ1
Topper's Solved these Questions
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( LONG ANSWER QUESTIONS )
12 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( NUMERICAL PROBLEMS )
40 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( VERY SHORT ANSWER QUESTIONS )
28 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
- PROPERTIES OF MATTERBOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (NUMERICAL PROBLEMS)
56 Videos
Similar Questions
Derive expressions for displacement, velocity and acceleration of a particle executing simple harmonic motion.
View SolutionWhich of the following functions represent SHM :
sin2ωt
View SolutionState the values of amplitude and frequency of a particle having the equation of simple harmonic motion as.
View SolutionWhat is meant by Parallax?
View SolutionA material breaks up under a stress of 20×105N/m2. If the density of the material is 2.5×103kg/m3, calculate the length may break under its own weight.(Take g=10m/s2)
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionThe phase difference between the instantaneous Velocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe phase of a particle executing simple harmonic motion is π2 when it has
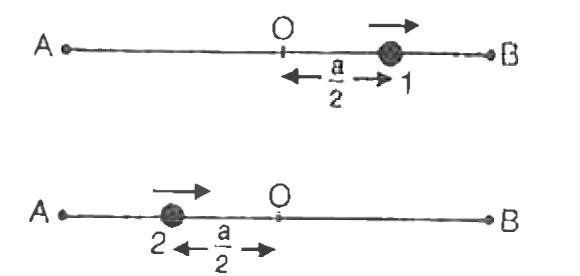
View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View SolutionA particle is executing two different simple harmonic motions, mutually perpendicular, of different amplitudes and having phase difference of pi//2 . The path of the particle will be
View SolutionThe phase difference between the instantaneous velocity & acceleration of a particle executing simple harmonic motion is
View SolutionIf a particle is executing simple harmonic motion, then acceleration of particle
View SolutionThe phase difference between the instantaneous velocity & acceleration of a particle executing simple harmonic motion is
View SolutionExplain by plats the position of particle executing simple harmonic motion at different time.
View Solution
