Explain by plats the position of particle executing simple harmonic motion at different time.Solution in Gujrati
The figure shows the positions of a particle executing S.H.M. are at discrete value to time, each interval of time being T4 where ϕ=0 and T is the period of motion.
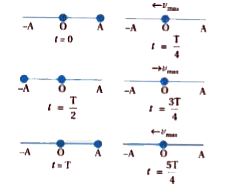
For a given SHM, A is the amplitude, then the velocity and position of a particle at time t is determine by the phase (ωt+ϕ) of cosine function.
In the equation of SHM x(t)=Acos(ωt+ϕ),ϕ=0 and ω=2πT,
x(t)=Acos(2πTt)
Now t=0
x(t)=Acos(0)=+A
Taking t=T4
x(t)=Acos(2πT×T4)=Acos(π2)=0
Taking t=T2
x(t)=Acos(2πT×T2)=Acosπ=−A
Taking t=3T4
x(t)=Acos(2πT×3T4)=Acos3π2=0
Taking t=T
x(t)=Acos(2πT×T)=Acos2π=+A
Taking t=5T4
x(t)=Acos(2πT×5T4)=Acos5π2=0
From figure got following observations :
(i) After period T, periodic (repeats) motion takes place.
(ii) Period T remains fixed no matter what location you choose as the initial (t=0) location.
(iii) The speed is maximum for zero displacement (at x=0) and zero at the extremes of motion (x= A).
Topper's Solved these Questions
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-A (TRY YOURSELF)
Explore 64 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
Explore 40 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Book:KUMAR PRAKASHANChapter:OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Exercise:CHAPTER - 8 (Match Type questions)
Explore 5 Videos
- PHYSICAL WORLDBook:KUMAR PRAKASHANChapter:PHYSICAL WORLDExercise:SECTION-E (QUESTIONS FROM MODULE)
Explore 9 Videos
Similar Questions
What is motion ?
View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionWhile a particle executes linear simple harmonic motion
View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
View SolutionIf a particle is executing simple harmonic motion, then acceleration of particle
View SolutionHow can the phase difference of two particles executing simple harmonic motions ?
View SolutionExplain the geometrical interpretation of simple harmonic motion. Also find the maximum and minimum values of velocity and acceleration for a particle executing simple harmonic motion.
View SolutionThe velocity of a particle executing simple harmonic motion is
View SolutionFor a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionThe total energy of a particle executing simple harmonic motion is
View SolutionThe total energy of a particle executing simple harmonic motion is:
View Solution