In figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ

(i) ΔABC~ΔPQR (Given)
So,ABPQ=BCQR=CARP (1)
and
∠A=∠P,∠B=∠Qand∠C=∠R (2)
But AB=2AM and PQ=2PN
(As CM and RN are medians)
So, from (1),
2AM2PN=CARP
i.e.,AMPN=CARP (3)
Also, ∠MAC=∠NPR [From (2)] (4)
So, from (3) and (4),
△AMC~△PNR (SAS similarity) (5)
(ii) From (5),CMRN=CARP (6)
But CARP=ABPQ [From (1)] (7)
Therefore, CMRN=ABPQ [From (6) and (7)] (8)
(iii) Again, ABPQ=BCQR [From (1)]
Therefore, CMRN=BCQR [From (8)] (9)
Also, CMRN=ABPQ=2BM2QN
i.e.,CMRN=BMQN (10)
i.e., CMRN=BCQR=BMQN [From (9) and (10)]
Therefore,△CMB~△RNQ(SSS similarity)
Topper's Solved these Questions
Similar Questions
In figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.
 View Solution
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively whereΔABC~ΔPQR, prove that ABPQ=ADPM
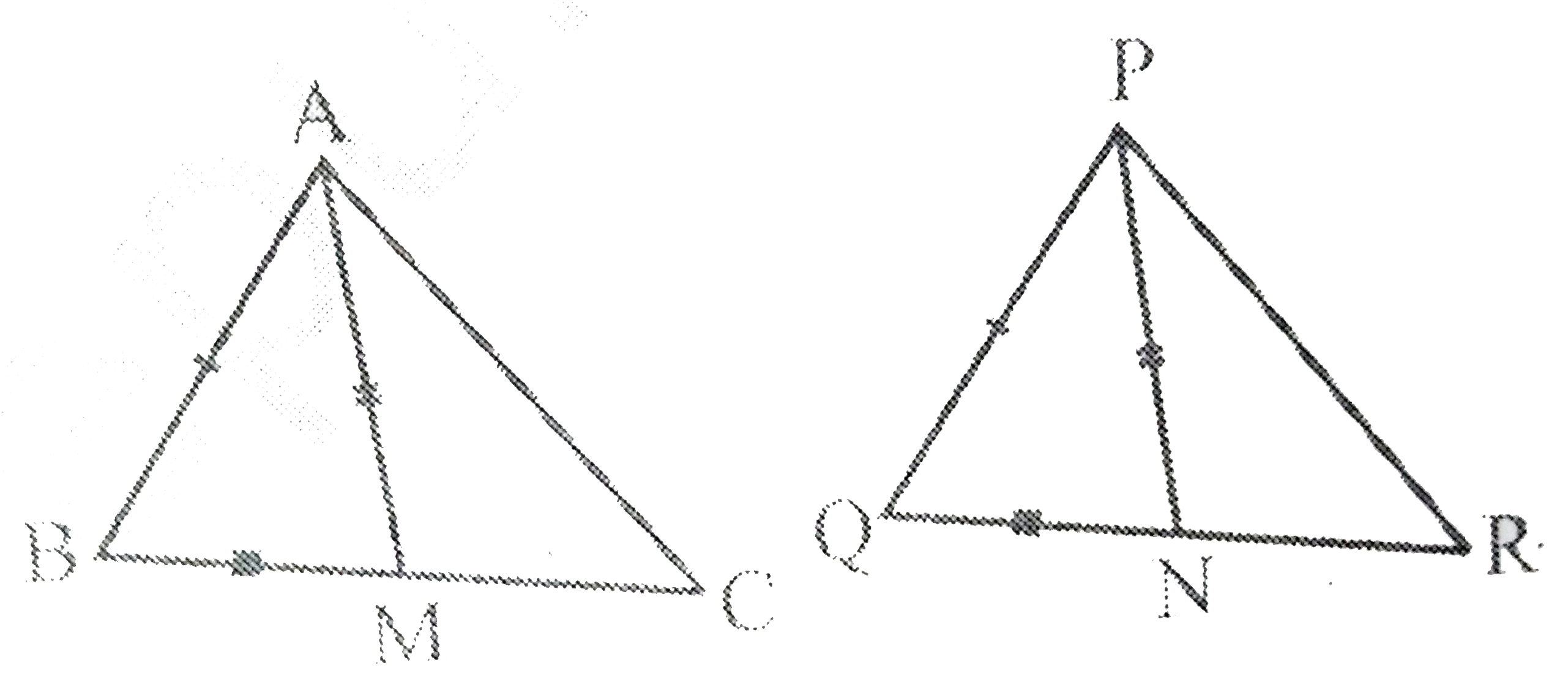
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
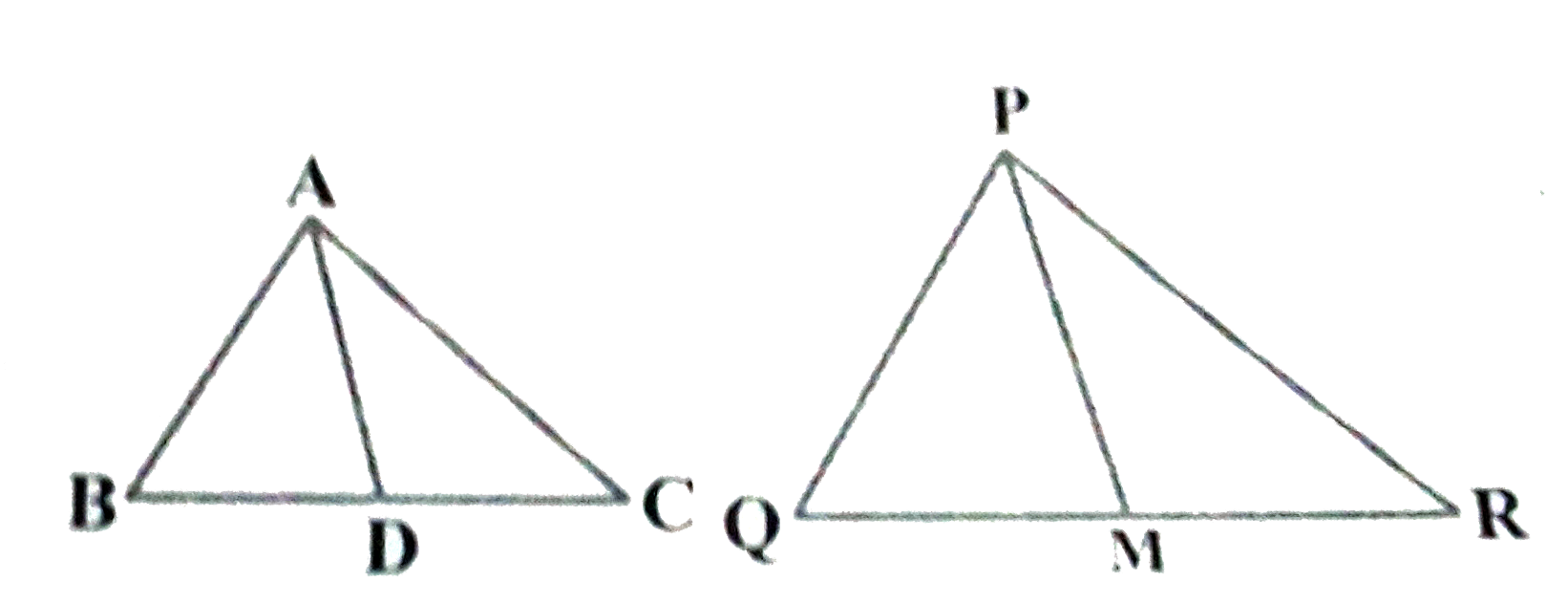
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
 View Solution
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
 View Solution
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
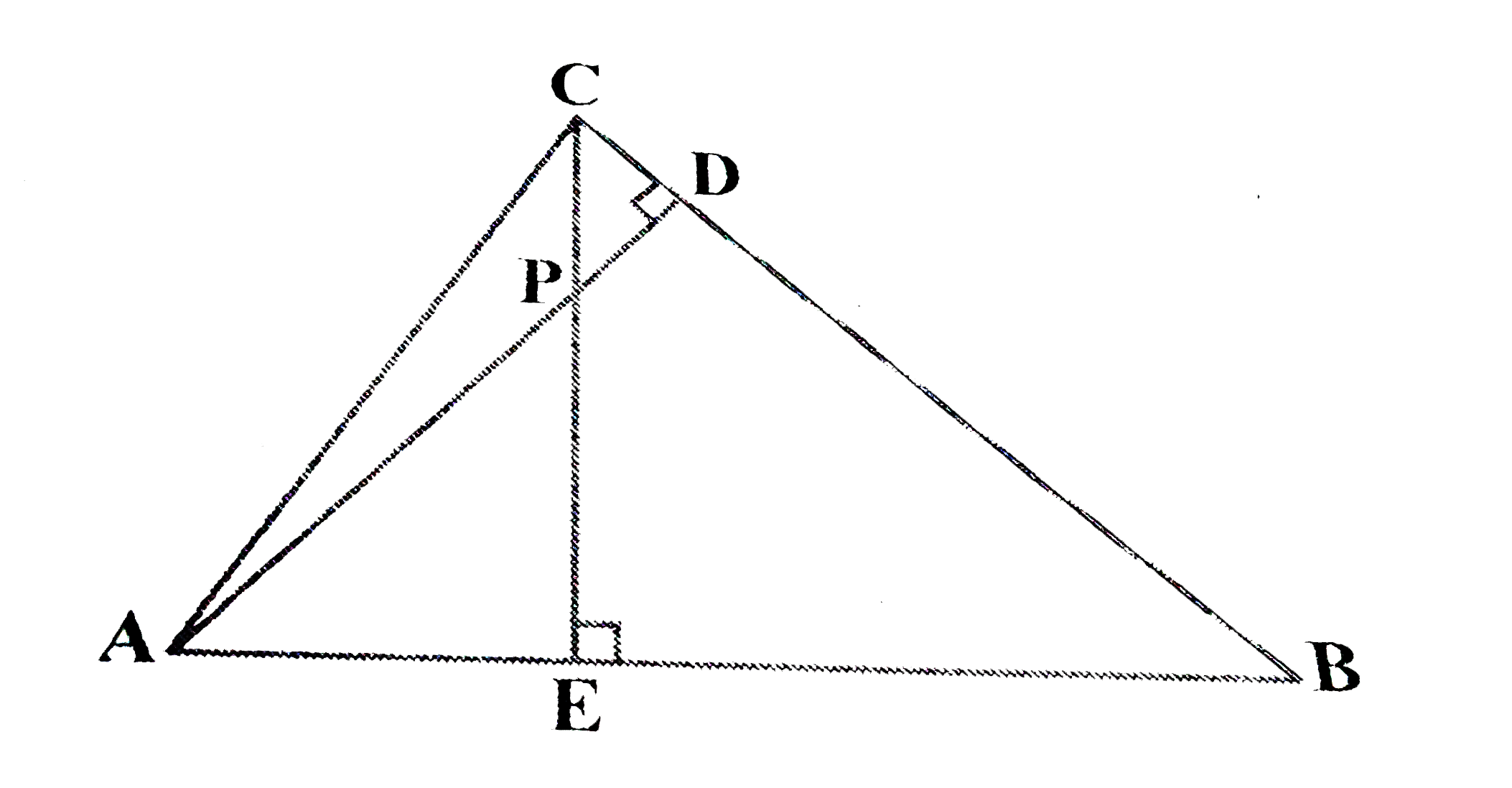
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
 View Solution
View SolutionIn fig., D is a point on hypotenuse AC of ΔABC,DM⊥BCand DN⊥AB. Prove that
(i) DM2=DN⋅MC
(ii) DN2=DM⋅AN
 View Solution
View Solution

