Let y=(3sinx) where x∈Randy∈[−3,5] then domain and range of g(x)=2+3f(2x+1) are [a,b]and[c,d] respectively then the value of (a+b+c+d) is equal to
Step by step video & image solution for Let y= (3 sin x) where x in R and y in [-3, 5] then domain and range of g(x) = 2 + 3f (2x + 1) are [a, b] and [c, d] respectively then the value of (a+ b+c+d) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let y=(3sinx) where x∈Randy∈[−3,5] then domain and range of g(x)=2+3f(2x+1) are [a,b]and[c,d] respectively then the value of (a+b+c+d) is equal to
View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
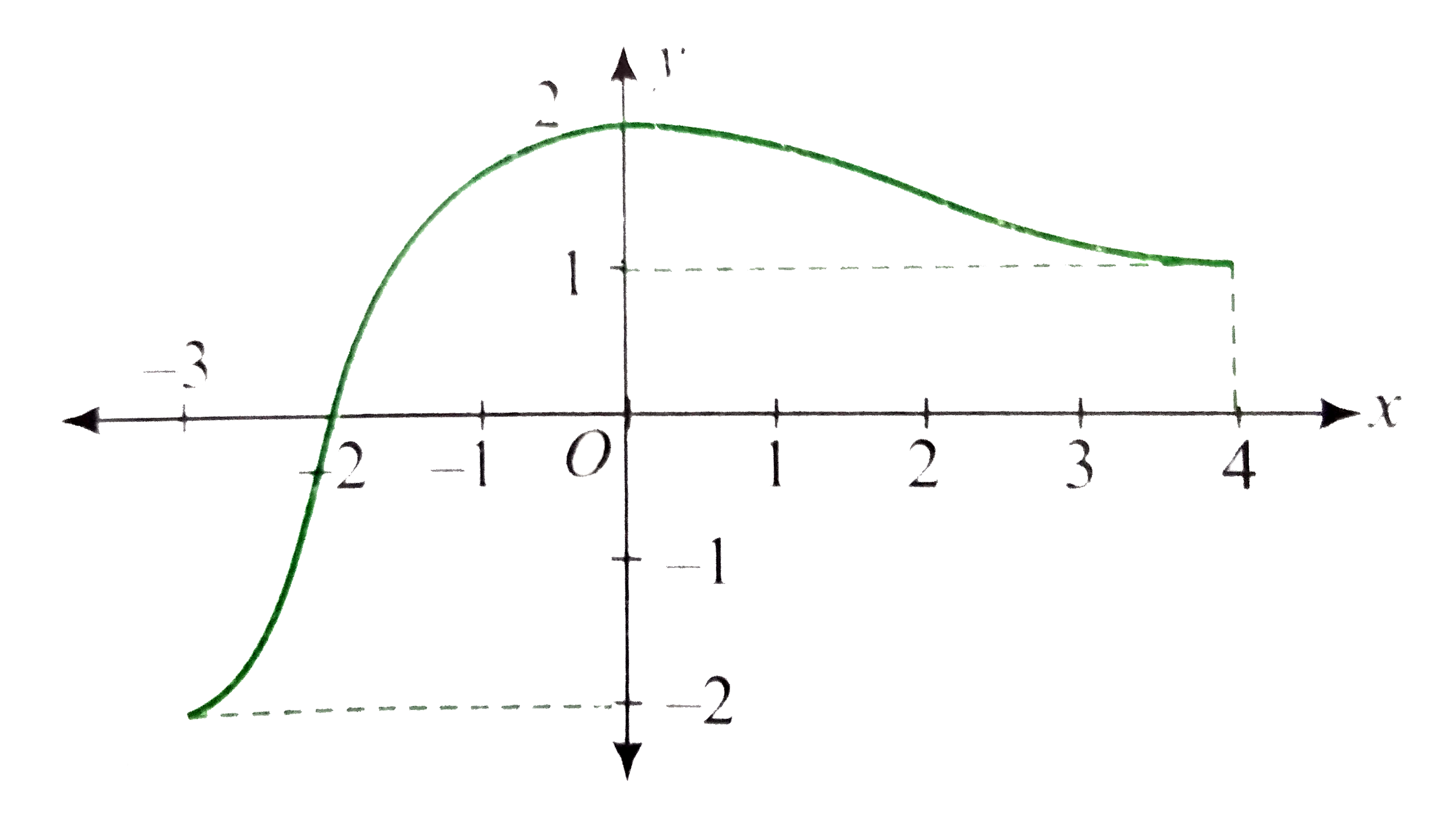
Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) is
View Solution
Knowledge Check
Consider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.

Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) isA11B10C8D7Domain and range of the function
f(x)=√sin−1(3x)+π3 is [a√3,b3] and [c,d√5π] respectively, then 2a + b + c + 6d is equal to-A1B2√3C√6Dnone of these
If the maximum and minimum values of y=x2−3x+cx2+3x+c are 7 and 17 respectively then the value of c is equal to (A) 3 (B) 4 (C) 5 (D) 6
View SolutionIf the maximum and minimum values of y=x2−3x+cx2+3x+c are 7 and 17 respectively then the value of c is equal to (A) 3 (B) 4 (C) 5 (D) 6
View SolutionLet f:R+→R be defined as f(x)=x2−x+2andg:[1,2]→[1,2] be defined as g(x)=[x]+1. Where [.] Fractional part function. If the domain and range of f(g(x)) are [a,b] and [c,d) then find the value of ba+dc.
View SolutionLet h(x)=|kx+5|,then domainof f(x) be [-5,7], the domain of f(h(x)) be[−6,1],and the range of h(x) be the same as the domain of f(x). Then the value of k is. (a)1 (b) 2 (c) 3 (d) 4
View SolutionLet h(x)=|kx+5|,then domainof f(x) be [-5,7], the domain of f(h(x)) be[−6,1],and the range of h(x) be the same as the domain of f(x). Then the value of k is. (a)1 (b) 2 (c) 3 (d) 4
View SolutionIf f:x→y, where xandy are sets containing natural numbers, f(x)=x+5x+2 then the number of elements in the domain and range of f(x) are, respectively. (a) 1and1 (b) 2and1 (c) 2and2 (d) 1and2
View Solution
