A block of mass m rests on a rough horizontl surface as shown in figure (a) and (b). Coefficient of friciton between block and surface is μ. A force F-mg acting at an angle θ with the vertical side of the block. Find the condition for which block will move along the surface.
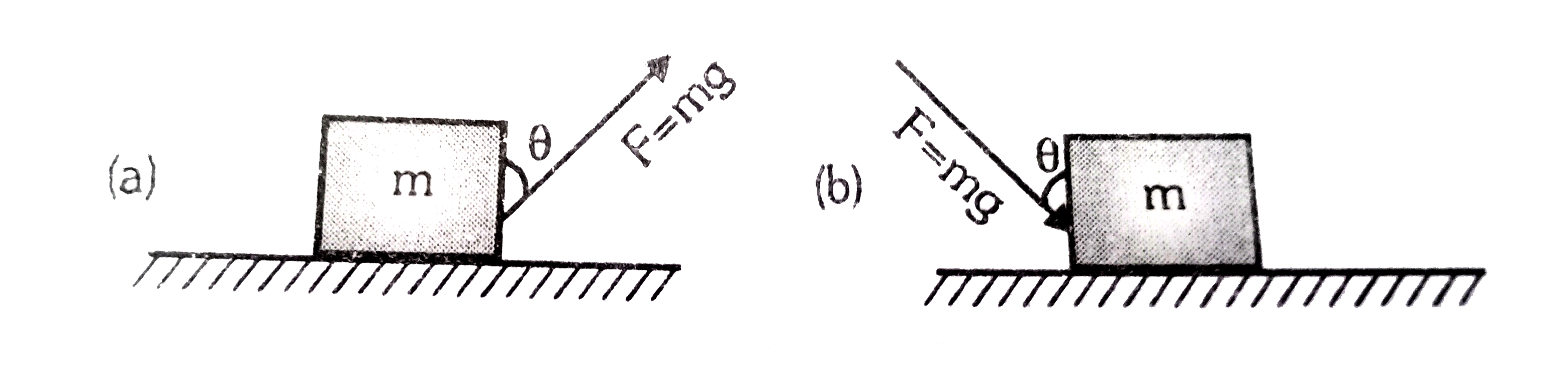
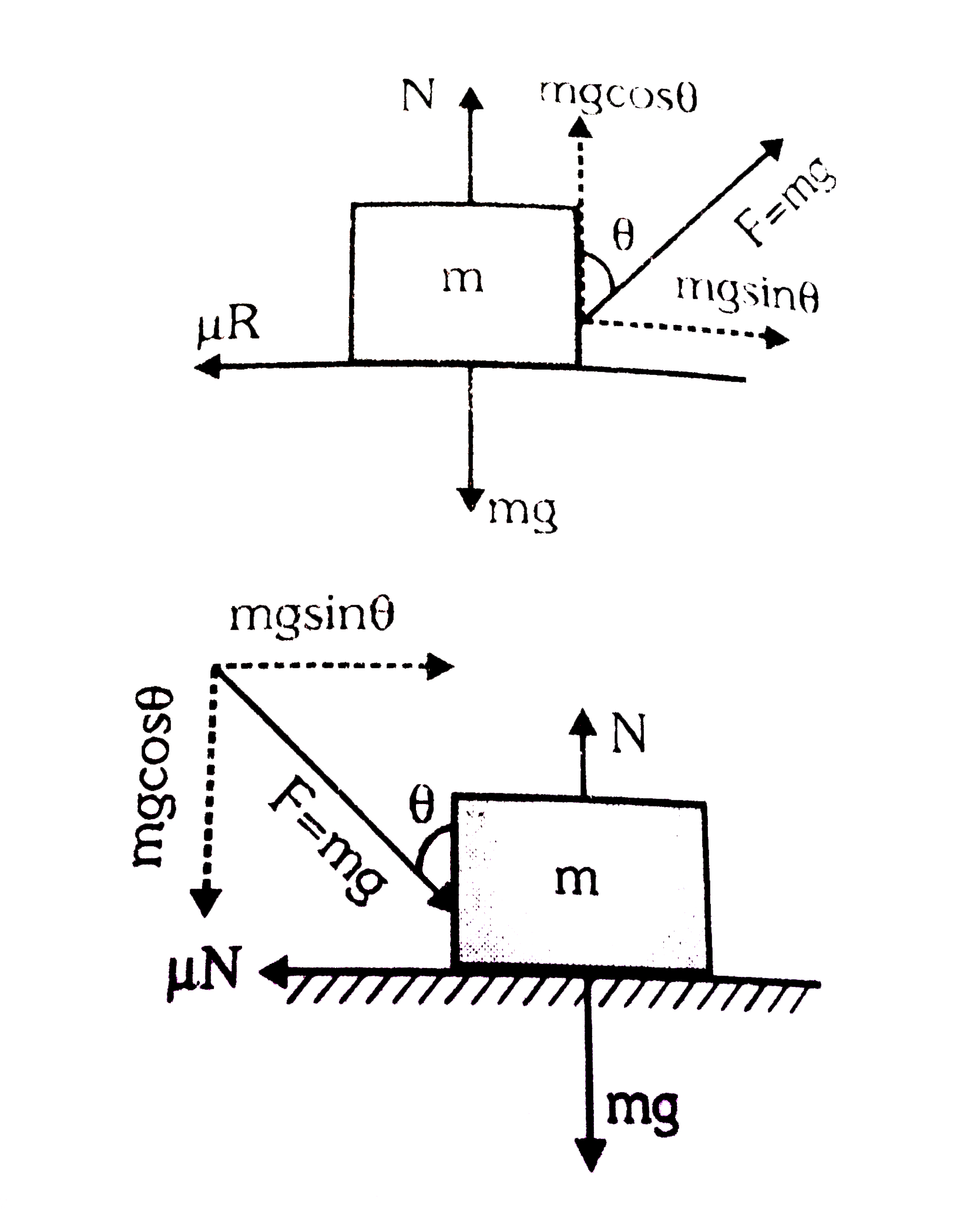
For(a): normal reaction N=mg−mgcosθ fricitional force =μN=μ(mg−mgcosθ)
Now block can be pulled when : Horizontal component of force ≥ fricitional force i.e. mgsinθ≥μ(mg−mgcosθ)
or 2sin(θ)2cos(θ)2≥μ(1−cosθ)
or 2sin(θ)2cos(θ)2≥2μsin2(θ)2 or cot(θ)2≥μ
For (b): Normal reaction N=mg+mgcosθ=mg(1+cosθ) Hence, block can be pushed along the horizontal surface when horizontal component of force ≥ fricitional force
i.e. mgsinθ≥μmg(1+cosθ) or
2sin(θ)2cos(θ)2≥μ×2cos2(θ)2⇒tan(θ)2≥μ
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
Similar Questions
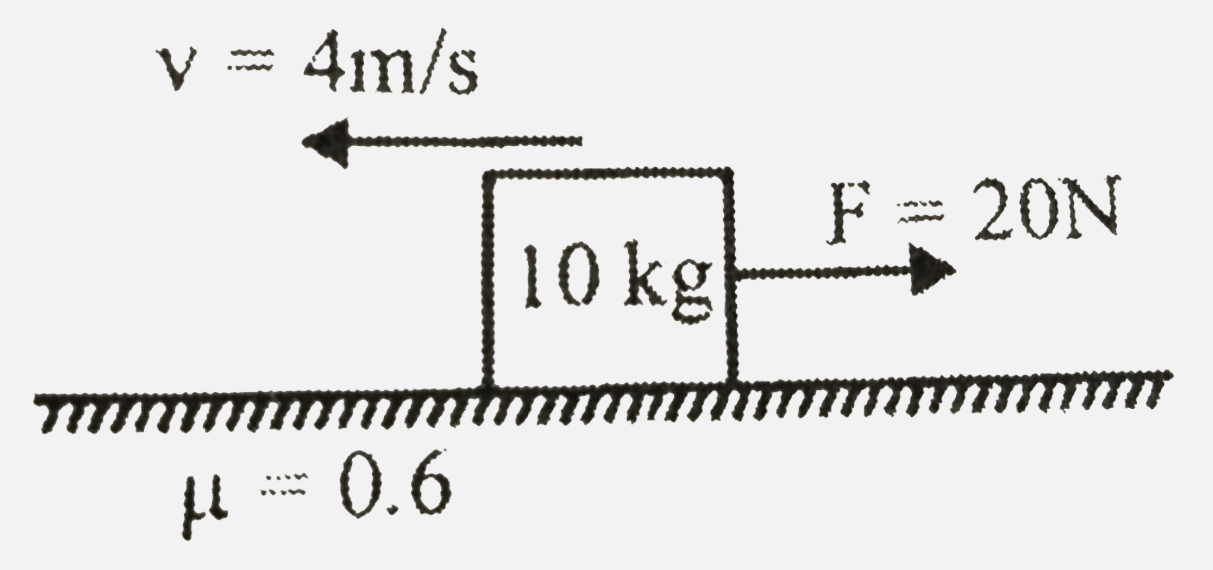
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
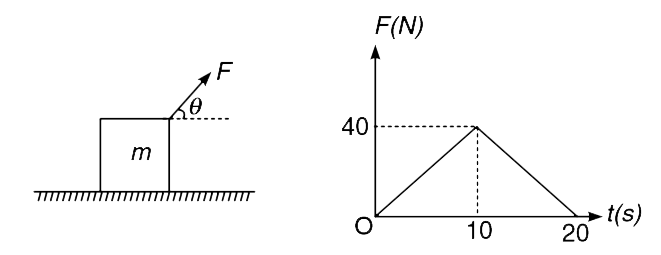
View SolutionA block of mass m=4.4kg lies on a horizontal rough surface. The coefficient of friction between the block and the surface is μ=0.5. A force F starts acting on the block making an angle θ=37∘ to the horizontal. The force changes with time as shown in the graph.
(a) At what time the block begins to move ?
(b) Calculate the maximum speed attained by the block.
[tan37∘=34,g=10ms−2]
View Solution
Knowledge Check
A block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is μ. A force F=mg acting at angle θ with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?
 Atanθ≥μBtan(θ2≥μ)Ccosθ≥μDcot(θ2)≥μ
Atanθ≥μBtan(θ2≥μ)Ccosθ≥μDcot(θ2)≥μA block of mass M is at rest on a rough horizontal surface. The coefficient of friction between the block and the surface is μ. A force F = Mg acting at an angle θ with the vertical side of the block pulls it. In which of the following cases, the block can be pulled along the surface?
Atanθ≥μBcotθ≥μCtanθ/2≥μDcotθ/2≥μA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
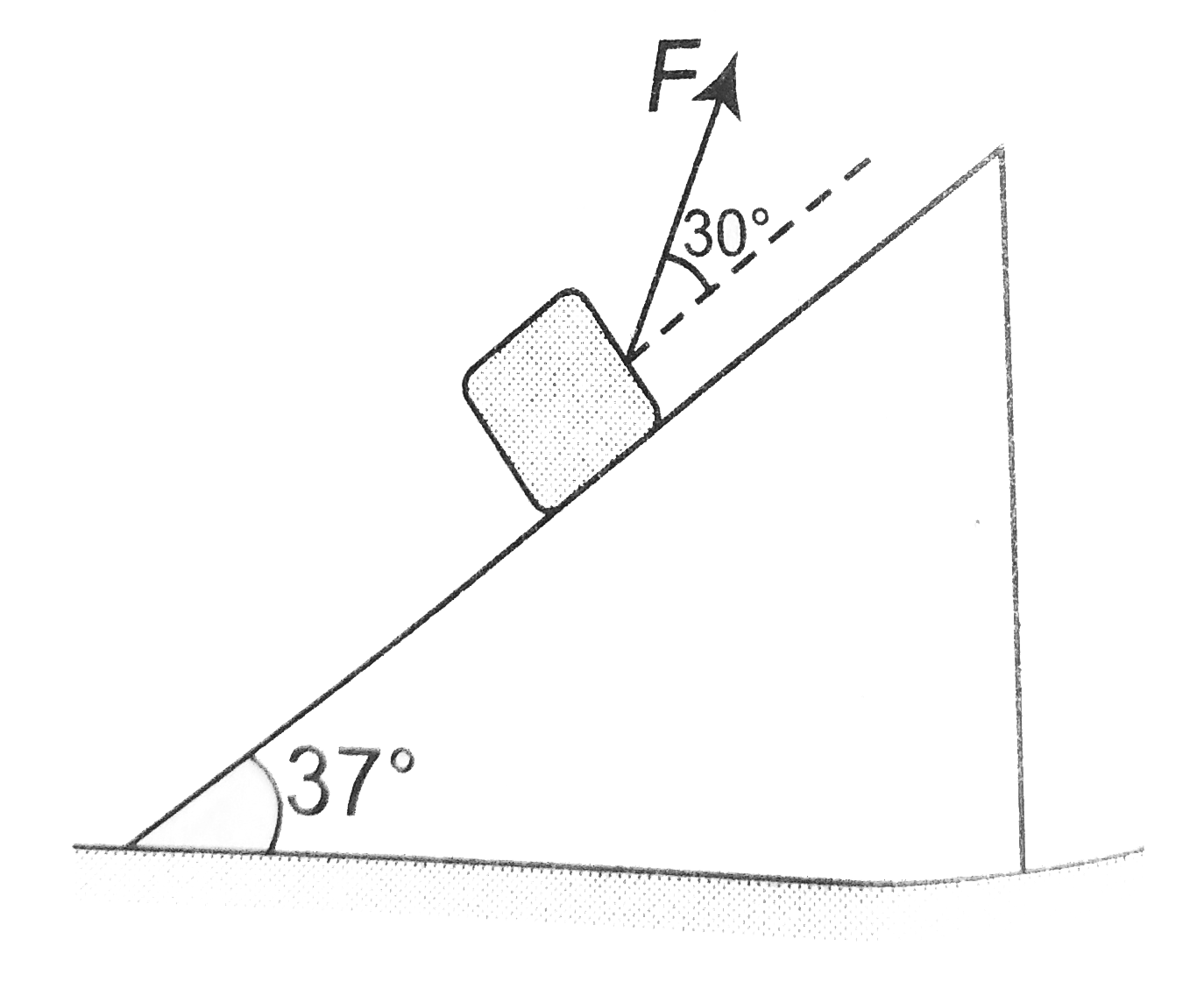
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:

View Solution