Blocks A and B of masses 5 kg and 10kg are placed as shown in figure. If block A is pulled with 50 N. Find out acceleration of the A and B. if coefficient of friction between A and B is 0.5and between B and ground is 0.4.
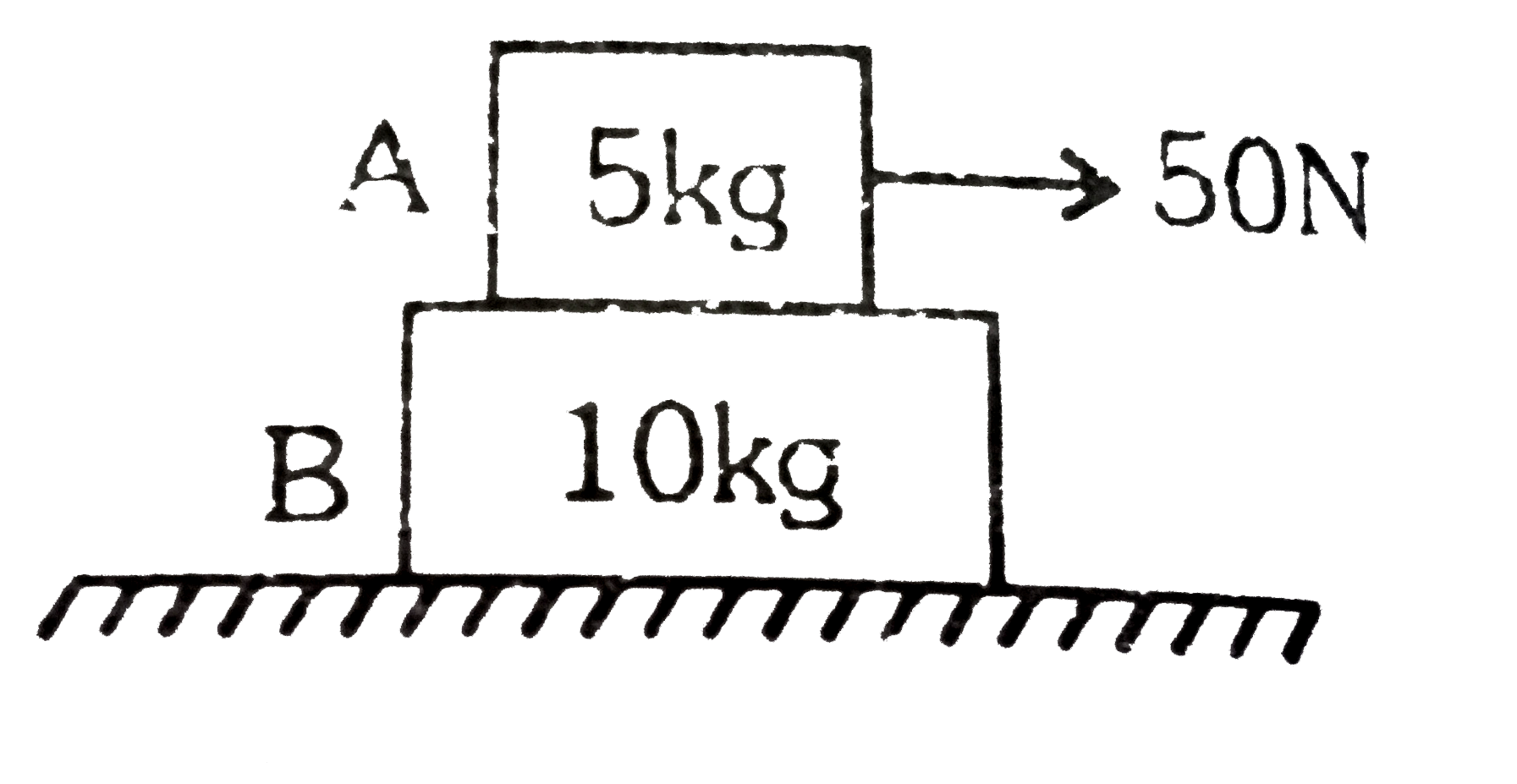
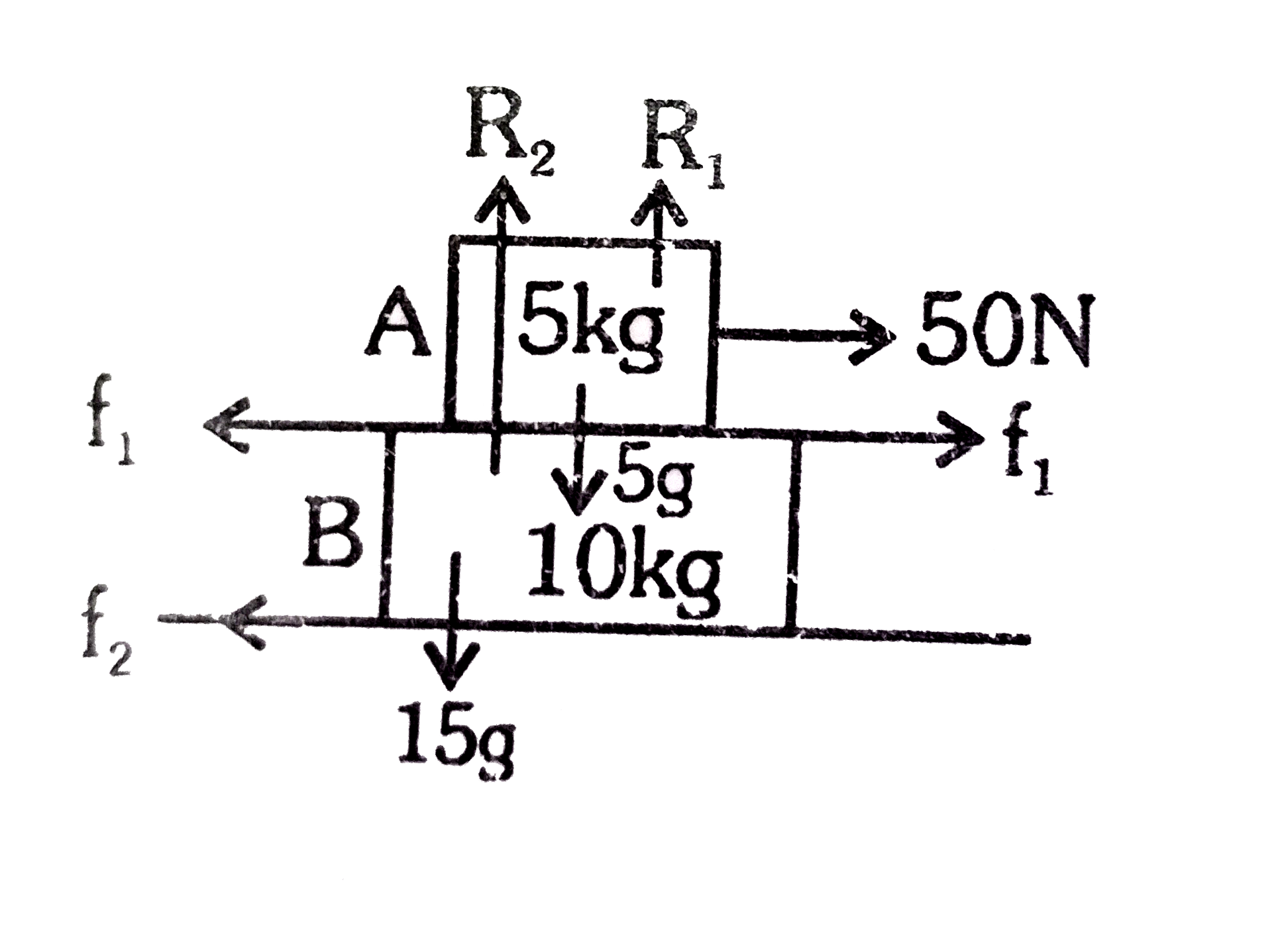
Limiting friction between A and B, f1=μ1R1=0.5×5g=24.5N
Limiting friction between B and ground f2=μ2R2=0.4×15g=58.8N
For block A50−f1=5×a⇒50−24.5=5×a⇒a=5.1m/s2
For block B accelerating force f1=24.5N is less than limiting friction f2=58.8N so block B will remain at rest.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I52videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II112videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
Similar Questions
Consider two blocks A and B of mass 3 kg and 9 kg respectively. Now, block A is placed on block B which is at rest on a table where the coefficient of friction between A and B is 0.4 and between B and the surface of the table is also 0.4. A force F is applied on B horizontally such that the block A does not slide over B. The maximum value of force F is ________N . (Take g=10m/s2)
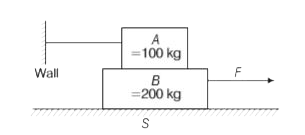
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Block A and B of masses 5 kg and 10 kg are placed as shown in figure. If block A is pulled with 50 N. Find out acceleration of the A and B. If coefficient of friction between A and B is 0.5 and between B and ground is 0.4.
 A5.1 and 0B4 and 0C3 and 2D3.2 and 5
A5.1 and 0B4 and 0C3 and 2D3.2 and 5 - Question 2 - Select One
A block A of mass 100 kg rests on another block B of mass 200 kg and is tied to a wall as shown in the figure. The coefficient of friction between A and B is 0.2 and that between B and ground is 0.3. The minimum force required to move the block B is (g=10ms−2)
 A900 NB200 NC1100 ND700 N
A900 NB200 NC1100 ND700 N - Question 3 - Select One
A block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.
 A900NB100NC1100ND1200N
A900NB100NC1100ND1200N
Two block A and B are arrenged as shown in figure (mA=5kgandmB=10kg) Find the acceleration of blocks if F=40N
 View Solution
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
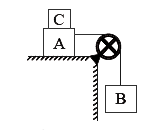 View Solution
View SolutionA block A of mass 200kg rest on a block B of mass 300kg. A is tied with a horizontal string to a wall. Coefficient of friction between A and Bis0.25 and that between B and floor is 0.2. The horizontal force F needed to move the block B is
 View Solution
View SolutionBlock AandB shown in the figure are connected with a bar of negligible weight. AandB each has mass 170kg , the coefficient of friction between A and the plane is 0.2 and that between B and the plane is 0.4(g=10ms−2)

What is the total force of friction between the blocks and the plane?View SolutionTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
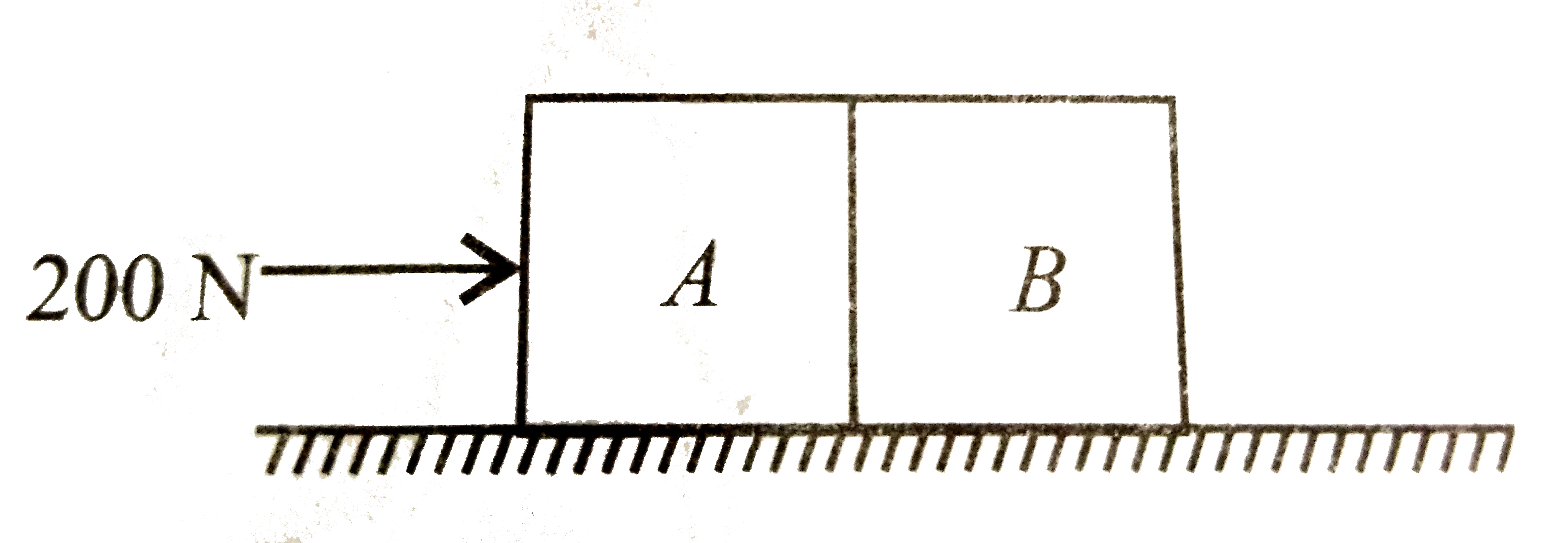 View Solution
View Solution

