A pendulum is suspended from the roof of a rall road car. When the car is moving on a circular track the pandulum inclines:
Forward
Backward
Towards the centre of the path
Away from the centre of the path
The correct Answer is:D
To solve the problem of a pendulum suspended from a railroad car moving on a circular track, we need to analyze the forces acting on the pendulum and how they affect its position.
1. Understand the Setup:
- A pendulum is hanging from the ceiling of a railroad car.
- The car is moving along a circular track.
2. Identify the Forces Acting on the Pendulum:
- The gravitational force (weight) acting downward, which is mg (where m is the mass of the pendulum bob and g is the acceleration due to gravity).
- The centripetal force required to keep the car moving in a circular path, which acts towards the center of the circular path.
3. Consider the Motion of the Car:
- As the car moves in a circular path, it experiences a centripetal acceleration directed towards the center of the circle.
- This means that the pendulum will not hang straight down; instead, it will be affected by the horizontal acceleration of the car.
4. Analyze the Pendulum's Position:
- The pendulum will experience a net force that is a combination of the gravitational force and the centripetal force acting towards the center of the circular path.
- The pendulum will therefore incline away from the vertical position, towards the outside of the circular path.
5. Determine the Direction of Inclination:
- Since the pendulum is experiencing a force that pulls it outward (due to the inertia of the pendulum bob as the car turns), it will incline away from the center of the circular path.
- Thus, the pendulum will be inclined outward, away from the center of the circular path.
6. Conclusion:
- The correct answer is that the pendulum inclines away from the center of the path.
Final Answer:
The pendulum inclines away from the center of the path (Option D).
---
- A pendulum is hanging from the ceiling of a railroad car.
- The car is moving along a circular track.
- The gravitational force (weight) acting downward, which is mg (where m is the mass of the pendulum bob and g is the acceleration due to gravity).
- The centripetal force required to keep the car moving in a circular path, which acts towards the center of the circular path.
- As the car moves in a circular path, it experiences a centripetal acceleration directed towards the center of the circle.
- This means that the pendulum will not hang straight down; instead, it will be affected by the horizontal acceleration of the car.
- The pendulum will experience a net force that is a combination of the gravitational force and the centripetal force acting towards the center of the circular path.
- The pendulum will therefore incline away from the vertical position, towards the outside of the circular path.
- Since the pendulum is experiencing a force that pulls it outward (due to the inertia of the pendulum bob as the car turns), it will incline away from the center of the circular path.
- Thus, the pendulum will be inclined outward, away from the center of the circular path.
- The correct answer is that the pendulum inclines away from the center of the path.
The pendulum inclines away from the center of the path (Option D).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I52videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
Similar Questions
Figure shows a pendulum suspended from the roof of a car that has a constant acceleration a relative to the ground. Find the deflection of the pendulum from the vertical as observed from the ground frame and from the frame attached with the car.
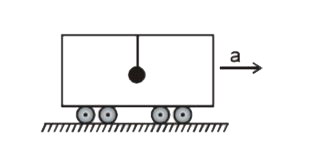 View Solution
View SolutionA simple pendulum of length l is suspended from the ceilling of a car moving with a speed v on a circular horizontal road of radius r. a. Find the tension in the string when it is at rest with respect to the car. b.Find the time period of small oscillation.
View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum is suspended from the roof of a train. If the train is moving with an acceleration 49cm/s2. Then the angle of inclination of the string about the vertical will be
A20∘BzeroC30∘D3∘ - Question 2 - Select One
A simple pendulum is suspended from the ceiling of a train which is moving with an acceleration a .The angular of inclination of the pendulum from the vertical will be
A90∘B0∘Ctan−1(ag)Dtan−1(ga) - Question 3 - Select One
A simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
AT=2π√lgBT=2π√lg+aCT=2π√l(g2+a2)DT=2π√lg−a
A simple pendulum of length l and having a bob of mass M is suspended ina car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium, what will be its time period ?
View SolutionA trolley moves in horizontal direction with an acceleration a. A simple pendulum of length l is suspended from the roof of the trolley. The time period of the pendulum will be
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
View SolutionA simple pendulum is suspended from the ceiling of a car and its period of oscillation is T when the car is at rest. The car starts moving on a horizontal road with a constant acceleration g (equal to the acceleration due to gravity, in magnitude) in the forward direction. To keep the time period same, the length of th pendulum
View SolutionThe period of oscillation of a simple pendulum of length / suspended from the roof of a vehicle, which moves without friction down an inclined plane of inclination α , is given by
View Solution

