The difference between lenghts of a certain brass rod and of a steel rod is claimed to be constant at all temperatures. Is this possible?
If LB and LS are the lengths of brass and steel rods respectively at a given temperature, then the lenghts of the rods when temperature is changed by θ.∘C.
L'B=LB(1+αBΔθ) and L'S=LS(1+αBΔθ). So that L'B−L'S=LB−LS+(LBαB−LSαS)Δθ
So (L'B−L'S) will be equal to (LB−LS) at all temperature if , LBαB−LSαS=0 [asΔθ≠0] or LBLS=αSαB
i.e., the difference in the lengths of the two rods will be independent of temperature if the lengths are in the
inverse ratio of their coefficients of linear expansion.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES84videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
One end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
AincreasesBdecreasesCremains constantDis non uniform. - Question 2 - Select One
A meter scale calibarated for temperature T is used to measure the length of a steel rod. Length of steel rod measured by metal scale at temperature 2T is L. Length of the rod measured by metal scale at temperature T is [αs:Coefficient of linear expansion of metal scale, αR : Coefficient of linear expansion of steel rod]
AL1+αsTBL(⊥+αRT)CL⊥+αRT(⊥+αST)DL(1+αST)(1+αRT) - Question 3 - Select One
The length of s steel rod exceeds that of a brass rod by 5 cm. If the difference in their lengths remains same at all temperature, then the length of brass rod will be: (α for iron and brass are 12×10−6/∘C and 18×10−6/∘C, respectively)
A15 cmB5 cmC10 cmD2 cm
A brass rod is 69.5 cm long and an aluminum rod is 49.0 cm long when both rods are at an initial temperature of 0∘C. The rods are placed in line with a gap of 1.5mm between them. The distance between the far ends of the rods remains same throughout. the temperapure is raised until the two rods are barely in contact. The coefficients of linear expansion of brass and aluminum are 2.0×10−5K−1 and 2.4×10−5K−1 respectively. In figure, the temperature at which contact of the rods barely occurs, in .∘C is closest to:
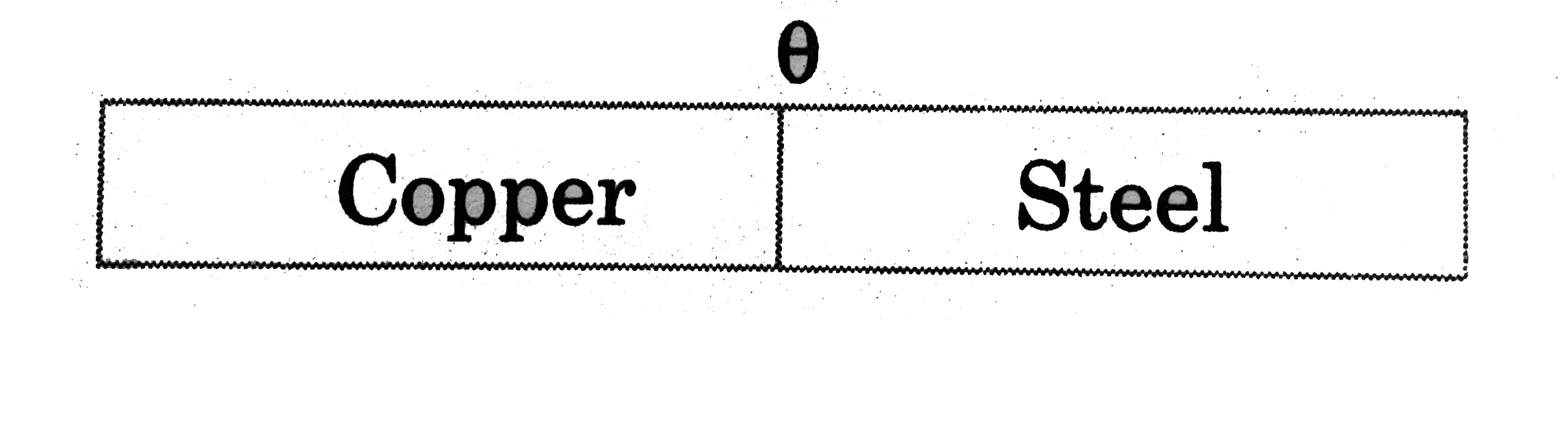
zView SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .
 View Solution
View SolutionThree rods of copper, brass and steel are welded together to form a Y -shaped structure. The cross-sectional area of each rod is 4cm2. The end of copper rod is maintained at 100∘C and the ends of the brass and steel rods at 80∘C and 60∘C respectively. Assume that there is no loss of heat from the surfaces of the rods. The lengths of rods are : copper 46 cm, brass 13 cm and steel 12 cm.
(a) What is the temperature of the junction point?
(b) What is the heat current in the copper rod?
K(copper) = 0.92, K (steel) = 0.12 and K(brass) = 0.26 cal/cm−s∘C .View SolutionA copper rod and steel rod having length Lc and Ls respectively at certain temperature. It is observed that difference between their length remains constant at all temperature. If αc and αs ar their respective coefficient of linear expansions. Then, ratio of LsLc is
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and equal cross-sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C. Find the temperature θ at the junction of the rods. Conductivity of copper
=390W/m−∘C and that of steel =46W/m−∘C.
 .View Solution
.View Solution