A certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
The initial temperature of ice is
−10∘C
−20∘C
−30∘C
−40∘C
The correct Answer is:D
Let heat is supplied at a rate of k1cal/min then
k1×1=m(0.5)θ1
k1×4=m(80) k1×2=m(1)(θ2)
⇒k1=20m⇒θ1=40∘C,θ2=40∘C
Therefore initial temperature =−40∘C
Final temperature = +40∘C
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A certain amount of ice is supplied heat at a constant rate for 7 minutes. For the first one minute the temperature rises uniformly with time. Then, it remains constant for the next 4 minute and again the temperature rises at uniform rate for the last two minutes. Calculate the final temperature at the end of seven minutes.
(Given, L of ice =336×(103)J/kg and specific heat of water =4200J/kg−K).
View SolutionHeat is supplied to a certain amount of ice at a constant rate for 9 min. For' the first 1 min, the temperature rises uniformly with time, Then the temperature remains constant for the next 5 min and after that again temperature rises at uniform rate for last 3min. If the ratio of magnitude of final temperature to initial temperature is P∘C, then find the 'value of 4P. (Given: S_ (ice )=0.5 (cal) (g)^(-1)/overset(o) \ C^(-1), L_(f)=80 (cal g).
View Solution
Knowledge Check
A certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
Final temperature at the end of 7 min isA10∘CB20∘CC30∘CD40∘CWhat amount of ice at −14∘C required to cool 200gg of water from 25∘C to 10CC?
(Given Cice=0.5calg.∘C,Lf for ice =80cal/g)A31gB41gC51gD21gHeat is being supplied at a constant rate to a sphere of ice which is melting at the rate of 0.1 gm/sec. It melts completely in 100 sec. The rate of rise of temperature thereafter will be (Assume no loss of heat)
A0.8.°C/secB5.4.°C/secC3.6.°C/secDwill change with time
In the above problem if heat is supplied at a constant rate of q=10cal/min, then plot temperature versus time graph.
View SolutionHeat is supplied to a ice at a constant rate Temperature variation with time is as shown in figure. Then –
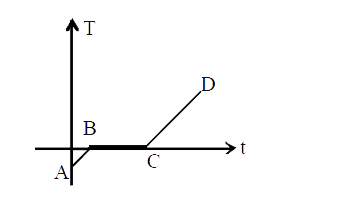
View SolutionHeat is being supplied at a constant rate to the sphere of ice which is melting at the rate of 0.1 gm/s. It melts completely in 100 s. The rate of rise of temperature thereafter will be
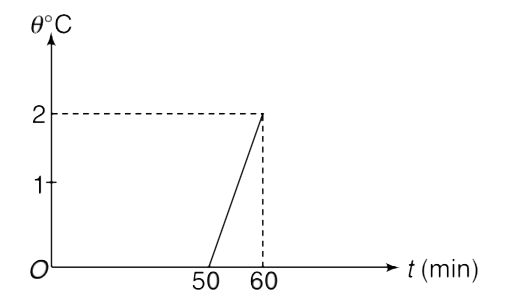
View SolutionA container contains 5 kg of water at 0∘C mixed to an unknown mass of ice in thermal equilibrium. The water equivalent of the container is 100 g. At time t = 0, a heater is switched on which supplies heat at a constant rate to the container. The temperature of the mixture is measured at various times and the result has been plotted in the given figure. Neglect any heat loss from the mixture – container system to the surrounding and calculate the initial mass of the ice.
Given: Sp. latent heat of fusion of ice is Lf=80calg−1
Sp. heat capacity of water =1calg−1.∘C−1
View SolutionFind the heat required to convert 20 g of iceat 0∘C into water at the same temperature. ( Specific latent heat of fusion of ice =80cal/g )
View Solution
