Calculate theta(1) and theta(2) in shown situation.

Topper's Solved these Questions

BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15videos
GEOMETRICAL OPTICS
BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73videos
GEOMETRICAL OPTICS
BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66videos
GEOMETRICAL OPTICS
BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427videos
CURRENT ELECTRICITY
BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9videos
GRAVITATION

Knowledge Check

Question 1 - Select One or More
Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

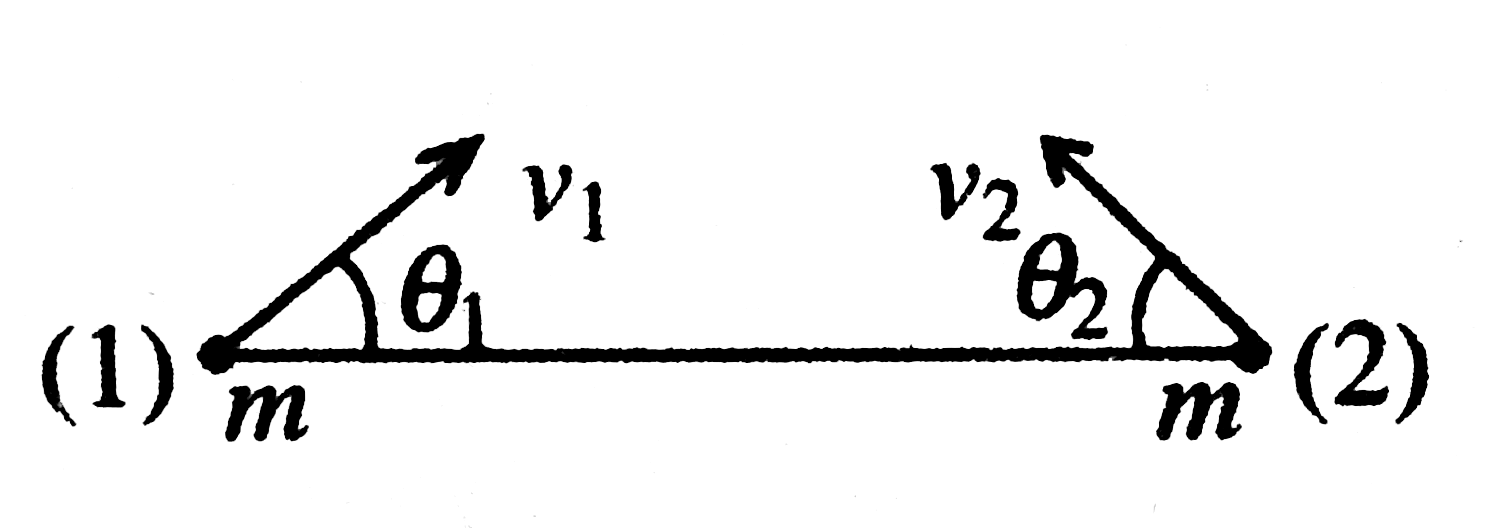ACentre of mass of particles will move along a vertical line.
BCentre of mass of particles will move along a line inclined at some angle with vertical.
CParticle $' 1'$ will be above vertical. centre of mass level when both particles are in air.
DParticle $' 2'$ will be above centre of mass level both particles are in air.
Question 2 - Select One
Two particles are projected from the same point with the same speed at different angles $θ_{1}$ and $θ_{2}$ to the horizontal. If their respective times of flights are $T_{1}$ and $T_{2}$ and horizontal ranges are same then
a) $θ_{1} + θ_{2} = 90^{\circ}$ ,
b) $T_{1} = T_{2} {tan θ}_{1}$
c. $T_{1} = T_{2} {tan θ}_{2}$ ,
d) $T_{1} {sin θ}_{2} = T_{2} {sin θ}_{1}$
A $a, b, d$ are correct
B $a, c, d$ are correct
C $b, c, d$ are correct
D $a, b, c$ are correct
Question 3 - Select One
Two particles of equal mass 'm' are projected from the ground with speed $v_{1}$ and $v_{2}$ at angles $θ_{1}$ and $θ_{2}$ at the same times as shown in figure. The centre of mass of the two particles.

Awill move in a vertical line if $v_{1} tan θ = v_{2} {tan θ}_{2}$
Bwill move in a vertical line if $v_{1} sin θ = v_{2} {sin θ}_{2}$
Cwill move In a vertical line if $v_{1} {cot θ}_{1} = v_{2} {cot θ}_{2}$
Dwill move in a vertical line if $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$

Calculate $θ_{1}$ and $θ_{2}$ in shown situation.

The correct Answer is: $θ_{1} = 116^{\circ} C, θ_{2} = 74^{\circ} C$

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

Two particles of equal mass 'm' are projected from the ground with speed $v_{1}$ and $v_{2}$ at angles $θ_{1}$ and $θ_{2}$ at the same times as shown in figure. The centre of mass of the two particles.

ALLEN-GEOMETRICAL OPTICS-EXERCISE - 04 (A)

Calculate θ1 and θ2 in shown situation.

The correct Answer is:θ1=116∘C,θ2=74∘C

In steady state rate of flow of heat in the whole system will be same . KA(200−θ1)l=2KA(θ1−θ2)l=15KA(θ2−18)l ⇒200−θ1=2θ1−2θ2 & 2θ1−2θ2=1.5θ2−27 ⇒θ1=116∘C,θ2=74∘C

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?

Two particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then a) θ1+θ2=90∘ , b)T1=T2tanθ1 c.T1=T2tanθ2 , d) T1sinθ2=T2sinθ1

Two particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.

ALLEN-GEOMETRICAL OPTICS-EXERCISE - 04 (A)

Calculate $θ_{1}$ and $θ_{2}$ in shown situation.

The correct Answer is: $θ_{1} = 116^{\circ} C, θ_{2} = 74^{\circ} C$

Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

Two particles of equal mass 'm' are projected from the ground with speed $v_{1}$ and $v_{2}$ at angles $θ_{1}$ and $θ_{2}$ at the same times as shown in figure. The centre of mass of the two particles.