An ideal gas in enclosed in a tube and is held in the vertical position with the closed end upward. The length of pellet of mercury entrapping the gas is h=10 cm and the length of the tube occupied by gas is l=40 cm. Calculate the length occupied by the gas when it is turned through θ=60∘ and 90∘. Atmospheric pressure , H=76 cm of mercury.
_E01_265_Q01.png)
The correct Answer is:37.2cm,34.7cm
For gas trapped in the tube P1V1=P2V2=P3V3
⇒(76−h)Al=(76−hcos60∘)Al=76×Al
⇒66×40=71×l'=76×l''l=37.2cm & l'=34.7cm
_E01_265_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)15videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)73videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions66videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
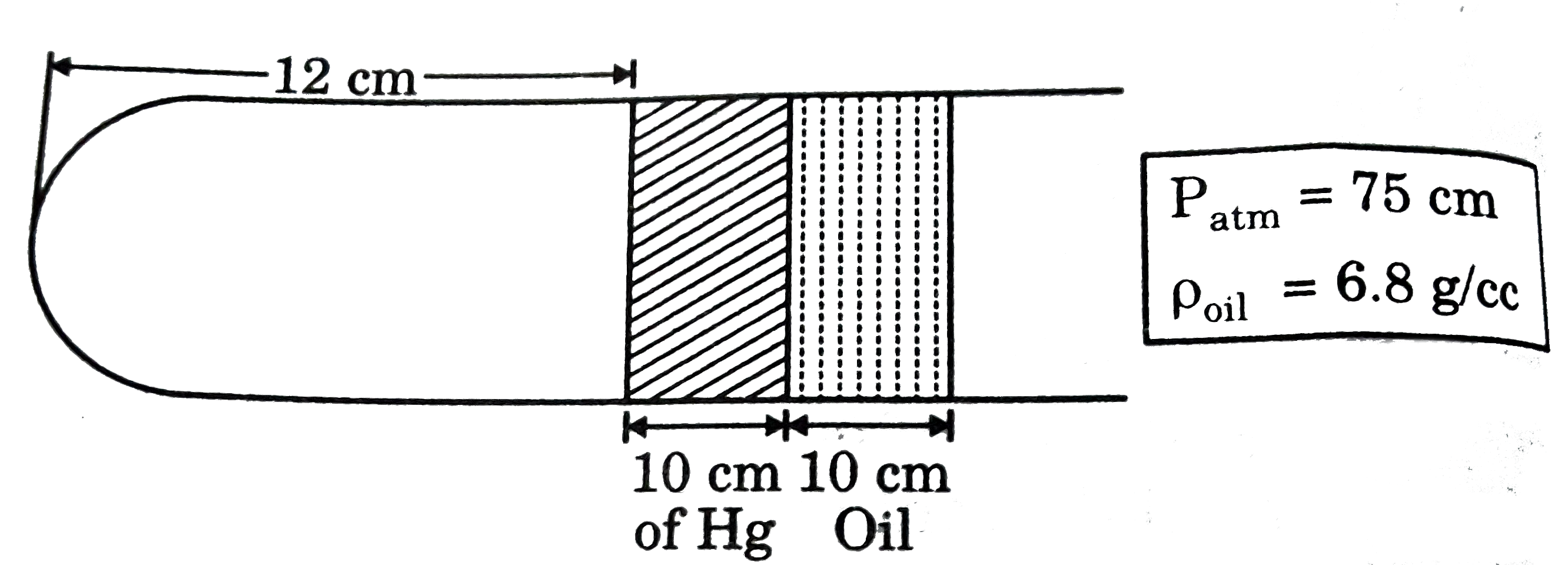
If above tube is held vertical with open end upward then find the length of air column (in cm).View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View Solution
Knowledge Check
- Question 1 - Select One
A mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
A37.5 cmB75cmC112.5cmD150cm - Question 2 - Select One
A mercury tube of length
100 cm. open at one end is kept
vertically with open end upwards. It
is filled with 10 cm of mercury to
trap an air column of height
40 cm. what will be the length of
trapped air if it is held vertically
with open end downwards ?
[ Assume atmospheric pressure to be 1 atm]A40.00 cmB32.00 cmC52.12 cmD82.00 cm - Question 3 - Select One
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)A38 cmB6 cmC16 cmD22 cm
A uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)
 View Solution
View SolutionA Quill's tube of one metre is taken. A certain amount of ideal gas is trapped in it by a 20 cm length of Hg column. When the tube is held vertical with open end upwards, the length of the gas column is 50 cm. Find the pressure and length of the trapped gas, when the Quill's tube is kept in slanting position making 45∘ with the vertical open and upwards. (Take atmospheric pressure as 76 cm of Hg and √2=1.414).
View SolutionAn open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)View Solution

