If one face of a prism angle 30∘andμ=√2 is silvered , the incident ray retraces its initial path. What is the angle of incidence?
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the configuration of the prism
We have a prism with an angle of 30 degrees, and one of its faces is silvered. This means that when light hits this face, it reflects back into the prism.
Step 2: Identify the angles involved
Let’s denote:
- The angle of the prism as A=30∘
- The refractive index μ=√2
- The angle of incidence at the first face of the prism as i
- The angle of refraction as r
Step 3: Use the property of reflection
Since the ray retraces its path after reflecting off the silvered face, the angle of incidence at the silvered face must be 90∘. This means that the angle of refraction at the first face must be such that it allows the ray to hit the silvered face at 90∘.
Step 4: Apply Snell's Law at the first face of the prism
Using Snell's Law at the first face (face AC):
n1sin(i)=μsin(r)
Here, n1=1 (air), so we have:
sin(i)=μsin(r)
Step 5: Relate angles using geometry
The angle of refraction r can be determined from the geometry of the prism. The angle r at the first face and the angle of the prism A are related as follows:
r=A−i
Substituting A=30∘:
r=30∘−i
Step 6: Substitute r into Snell's Law
Now substituting r in Snell's Law:
sin(i)=√2sin(30∘−i)
Since sin(30∘)=12:
sin(i)=√2(sin(30∘)cos(i)−cos(30∘)sin(i))
This simplifies to:
sin(i)=√2(12cos(i)−√32sin(i))
Step 7: Rearranging the equation
Rearranging gives:
sin(i)+√32√2sin(i)=√22cos(i)
Factoring out sin(i):
sin(i)(1+√32√2)=√22cos(i)
Step 8: Solve for i
After some calculations, we find that:
sin(i)=1√2⟹i=45∘
Conclusion
Thus, the angle of incidence i is 45∘.
---
We have a prism with an angle of 30 degrees, and one of its faces is silvered. This means that when light hits this face, it reflects back into the prism.
Let’s denote:
- The angle of the prism as A=30∘
- The refractive index μ=√2
- The angle of incidence at the first face of the prism as i
- The angle of refraction as r
Since the ray retraces its path after reflecting off the silvered face, the angle of incidence at the silvered face must be 90∘. This means that the angle of refraction at the first face must be such that it allows the ray to hit the silvered face at 90∘.
Using Snell's Law at the first face (face AC):
n1sin(i)=μsin(r)
Here, n1=1 (air), so we have:
sin(i)=μsin(r)
The angle of refraction r can be determined from the geometry of the prism. The angle r at the first face and the angle of the prism A are related as follows:
r=A−i
Substituting A=30∘:
r=30∘−i
Now substituting r in Snell's Law:
sin(i)=√2sin(30∘−i)
Since sin(30∘)=12:
sin(i)=√2(sin(30∘)cos(i)−cos(30∘)sin(i))
This simplifies to:
sin(i)=√2(12cos(i)−√32sin(i))
Rearranging gives:
sin(i)+√32√2sin(i)=√22cos(i)
Factoring out sin(i):
sin(i)(1+√32√2)=√22cos(i)
After some calculations, we find that:
sin(i)=1√2⟹i=45∘
Thus, the angle of incidence i is 45∘.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES84videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
If one face of a prism angle 30∘ and μ=√2 is silvered, the incident ray retraces its initial path. What is the angle of incidence ?
View SolutionA ray of light incident on an equilateral triangular glass prism of μ=√3 moves parallel to the base of the prism inside it. What is the angle of incidence for this ray ?
View Solution
Knowledge Check
- Question 1 - Select One
One of the refracting surfaces of a prism of angle 30∘ is silvered. A ray of light incident at angle of 60∘ retraces its path. The refractive index of the material of prism is
A√2B√3C3/2D2 - Question 2 - Select One
The prism shown in the figure has one side silvered. The angle of the prims is 30∘ and μ=√2. What should be the angle of incidence, if the incidence ray retraces its initial path?
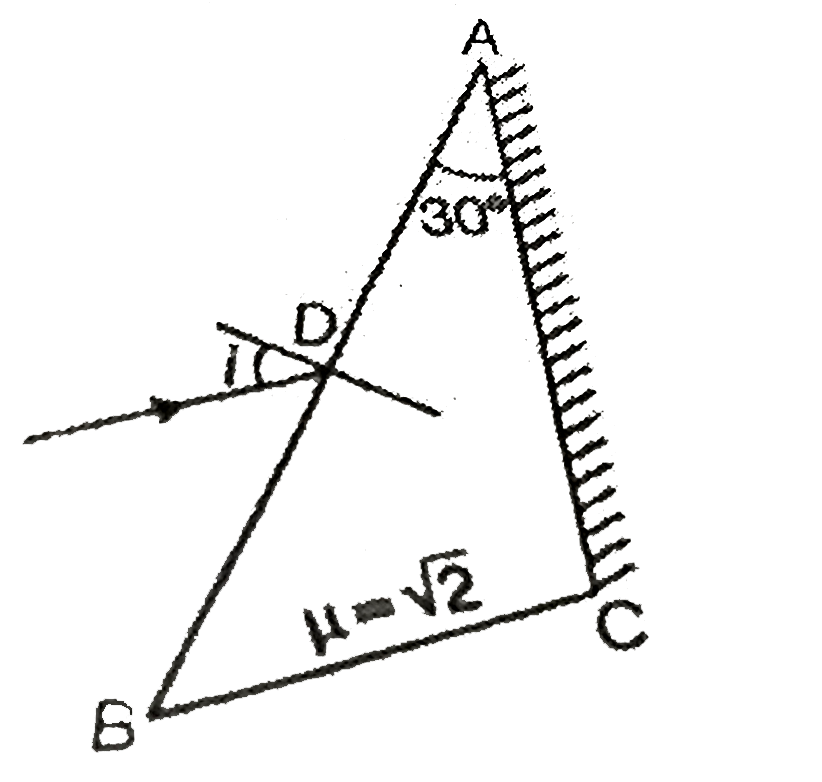 A50∘B45∘C60∘D75∘
A50∘B45∘C60∘D75∘ - Question 3 - Select One
One of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
A√2B√3C3/2D2
The refractives index of the materials of a prism is √2and its prism angle is30∘One of its refracting faces is polished .The incident beam of light will return back for the angle of incidence
View Solution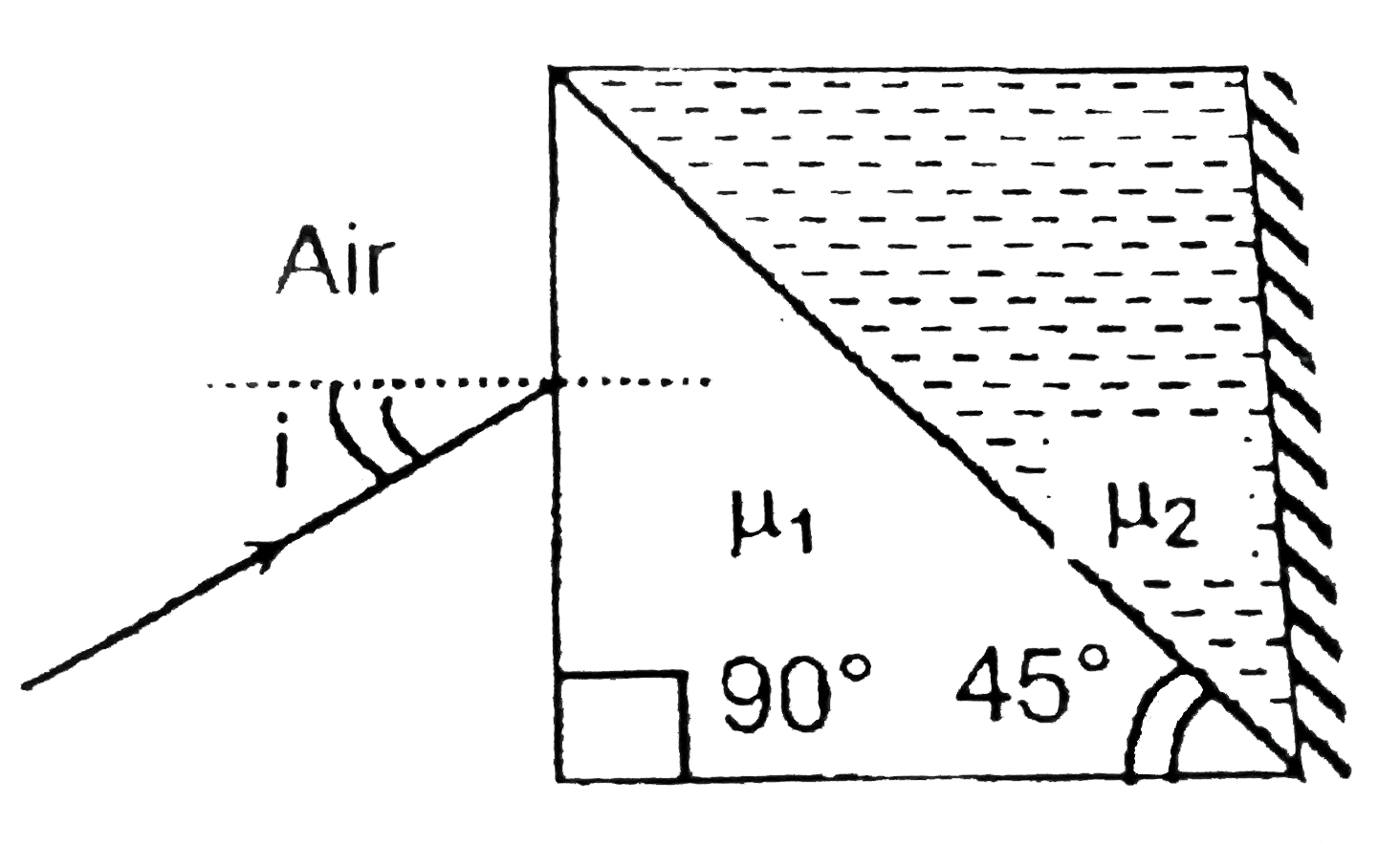
In the given situation, for what value of i, the incidence ray will retrace its initial path.View SolutionA ray passes through a prism of angle 60∘ in minimum deviation position and suffers a deviation of 30∘. What is the angle of incidence on the prism
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View SolutionA ray of light is incident on one face of a prism at an angle of 50∘ with the normal . The ray is deviated by the prism through 42∘ . What is the angle of the prism , if the angle of emergence is 51∘ ?
View Solution

