In a thin spherical fish bowl of radius 10 cm filled with water of refractive index (4/3) , there is a small fish at a distance 4 cm from the centre C as shown in Figure. Where will the fish appear to be, if seen from (a) E and (b) F (neglect the thickness of glass)?
_S01_020_Q01.png)
In the case of refraction from curved surface μ2v−μ1u=(μ2−μ1R
(a) Seen from Eμ1=43,μ2=1,R=−10cm & u=−(10−4)=−6cm
⇒1v−43−6=1−43−10⇒v=9017=−5.3cm
i.e., fish will appear at a distance 5.3 cm from E towards F (lesser than actual distance i.e., 6 cm)
(b) Seen from Fμ1=43,μ2=1,R=−10cm andu=−(10+4)=−14cm
⇒1v−43−14=1−43−10⇒v=−21013=−16.154cm
so fish will appear at a distance 16.154 cm from F toward E (more than actual distance , i.e., 14 cm)
_S01_020_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES84videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
In a spherical paper weight (R = 10 cm) made of glass of refractive index μ=32, an object is embedded at a distance 5 cm from its centre. What is the apparent position of the object when seen from the opposite side (see figure)?
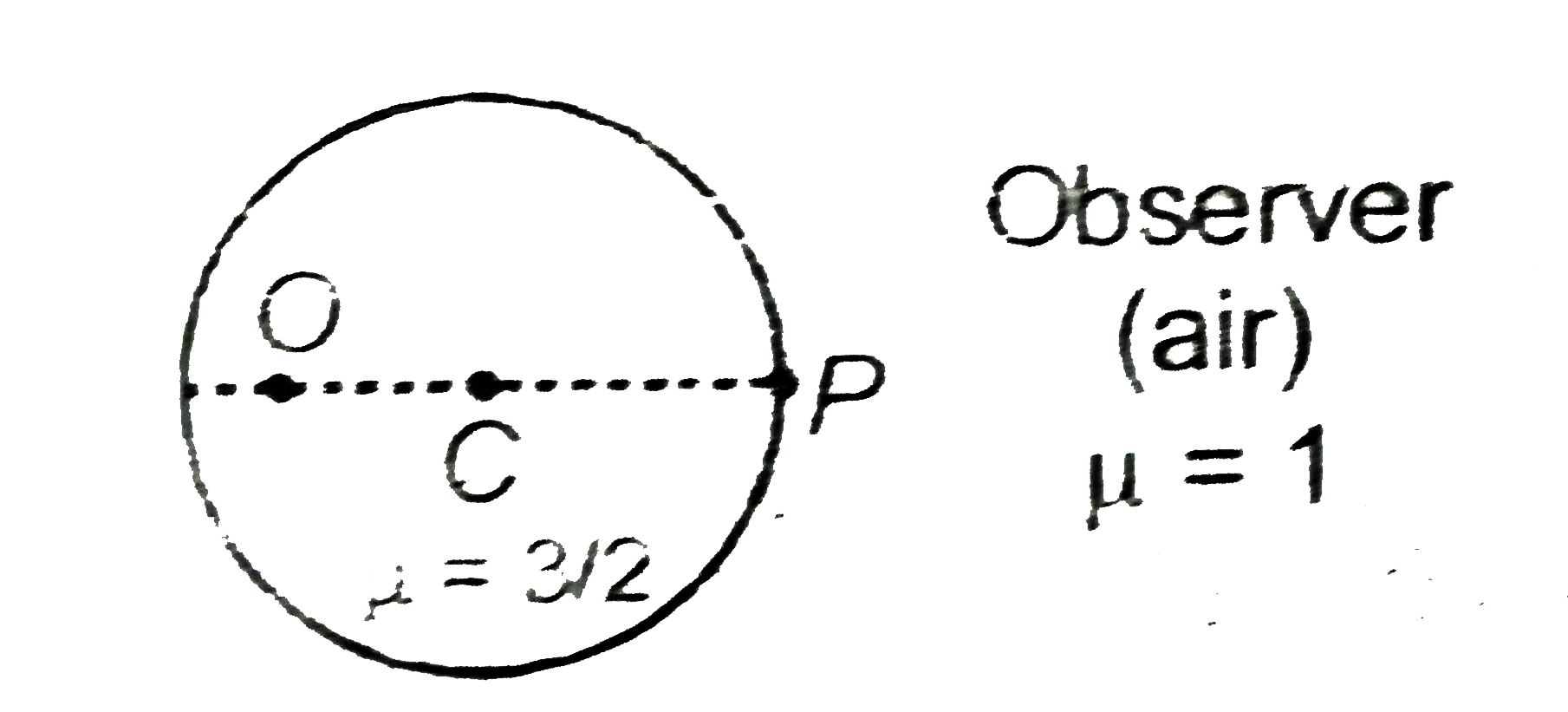 View Solution
View SolutionA hollow, spherical conductor of radius 10 cm is charged with 5×10−9C. Find the potential (a) at a distance of 20 cm from the centre ,(b) at the surface of the sphere , (c) at a distance of 5 cm from centre.
View Solution
Knowledge Check
- Question 1 - Select One
In a thin spherical fish bowl of radius 10 cm filled with water of refractive index 4/3 there is a small fish at a distance of 4 cm from the centre C as shown in the figure. Where will the image of fish appears, if seen from E.
 A5.2cmB7.2cmC4.2cmD3.2cm
A5.2cmB7.2cmC4.2cmD3.2cm - Question 2 - Select One
In a thin spherical fish bowl of radius 10 cm filled with water of refractive index 4/3 there is a small fish at a distance of 4 cm from the centre C as shown in figure. Where will the image of fish appears, if seen from E
 A5.2 cmB7.2 cmC4.2 cmD3.2 cm
A5.2 cmB7.2 cmC4.2 cmD3.2 cm - Question 3 - Select One
An object is placed at 24 cm distant from a surface of a lake. If water has refractive index of 4/3, then at what distance from the lake surface, a fish will get sight of an object.
A32 cm above the surface of waterB18 cm over the surface of waterC6 cm over the surface of waterD6 cm below the surface of water
A dust particle is inside a sphere of refractive index 43. If the dust particle is 10.0cm from the wall of the 15.0cm radius bowl, where does it appear to an observer outside the bowl.
View SolutionA spherical fish bowl of radius R is placed in front of a plane vertical mirror (M) The thickness of the wall of the fish bowl is very thin The centre (C) of the spherical bowl is at distance of 3R from the plane mirror. The bowl is filled with water and contains a fish (F) Fish(F) is at a distance of R from the centre of the spherical bowl as shown in the figure Refractive index of water is 4/3 two surfaces are indicated in the bowl as first surface (1) and second surface(2)

Column-IColumn-IIOptical Event–––––––––––––––Nature of image––––––––––––––––––(A)Refraction at first surface(P)Virtual(B)Refraction at second surface after reflection from mirror(Q)Real(C)Refraction at first surface after reflectionfrom mirror and refraction from second surface(R)Magnified(S)DiminishedView SolutionA fish bowl of diameter 20 cm is filled with a liquid of refractive index 1.4. A letter O is written on the outer surface of the bowl. Determine the position of the image of the word formed when observed through the bowl from the opposite side.
View SolutionThe charges given to a hollow sphere of radius 10 cm is 10 n C . Electric field at a point situated at a distance of 4 cm from its centre is
View SolutionA small object is enclosed in a sphere of solid glass 8cm in radius. It is situated 2cm from the centre and is viewed from the side of which it is nearer. Where will it appear to be if μ of glass =1.5/
View Solution

