A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
2000m
390m
infinite distance
None of these
The correct Answer is:A
μsinθ=μ0sin90∘=μ0⇒sinθ=μ0μ=1√1+ay
But dxdy=tanθ⇒dx=(dy)(1√ay)⇒x=1√a2∫01√ydy=[2√ya]20=2000m
_S01_052_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -01
Explore 65 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
A man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionOn a hot summer day in a desert the refractive index of the atmosphere changes with height (y) above the surface of the earth as μ=m0(1+by)1/2 where m0 is the refractive index at the surface and b=6×x10−4m−1. A man of height 1.5 m is standing on a straight level road. Calculate the distance beyond which he cannot see a point on the road.
View Solution
Knowledge Check
The wave number of a beam of light in air is 2.5×106 per metre. What is its wavelength in glass of refractive index 1.6 ?
A2000ÅB2500ÅC2750ÅD3000ÅA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
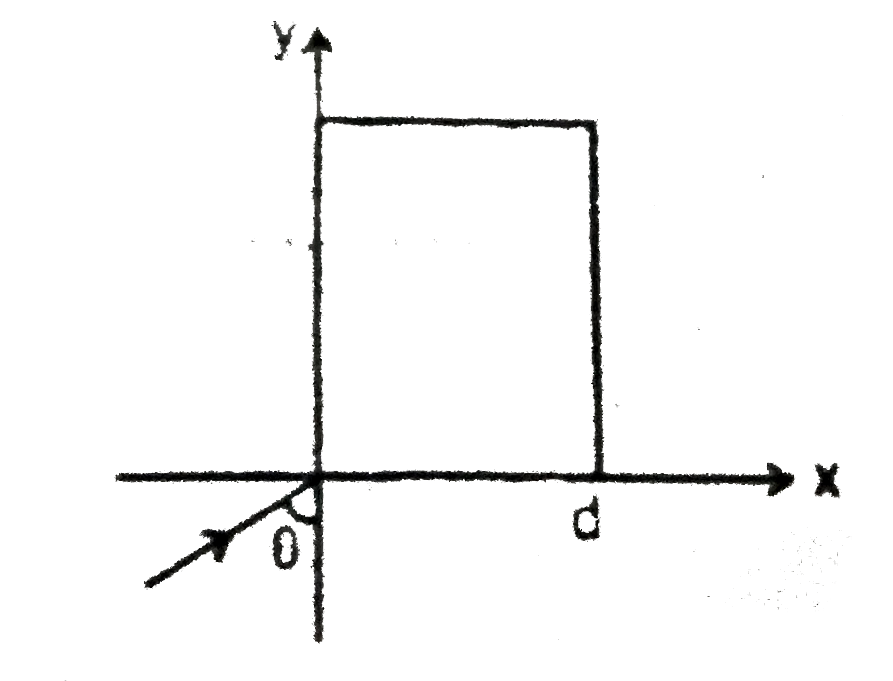 Ad(1−sinθ)Bd(1−cosθ)CdsinθDdcosθ
Ad(1−sinθ)Bd(1−cosθ)CdsinθDdcosθThe speed of light in air is 3×108m/s. What will be its speed in diamond whose refractive index is 2.4
A3×108m/sB332m/sC1.25×108m/sD7.2×108m/s
Due to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

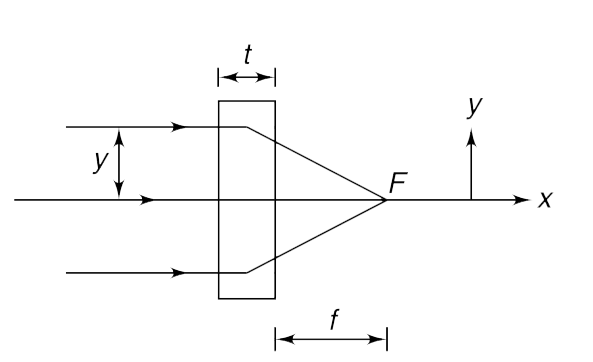
View SolutionA parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as μ=μ0(1–y2y02)where μ0 is the refractive index along x axis and y0 is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assumef>>t and consider y to be small.
View SolutionFind the velocity of light in water, if its velocity in glass of refractive index 1.5 is 2×108m/s. The refractive index of water is 1.33.
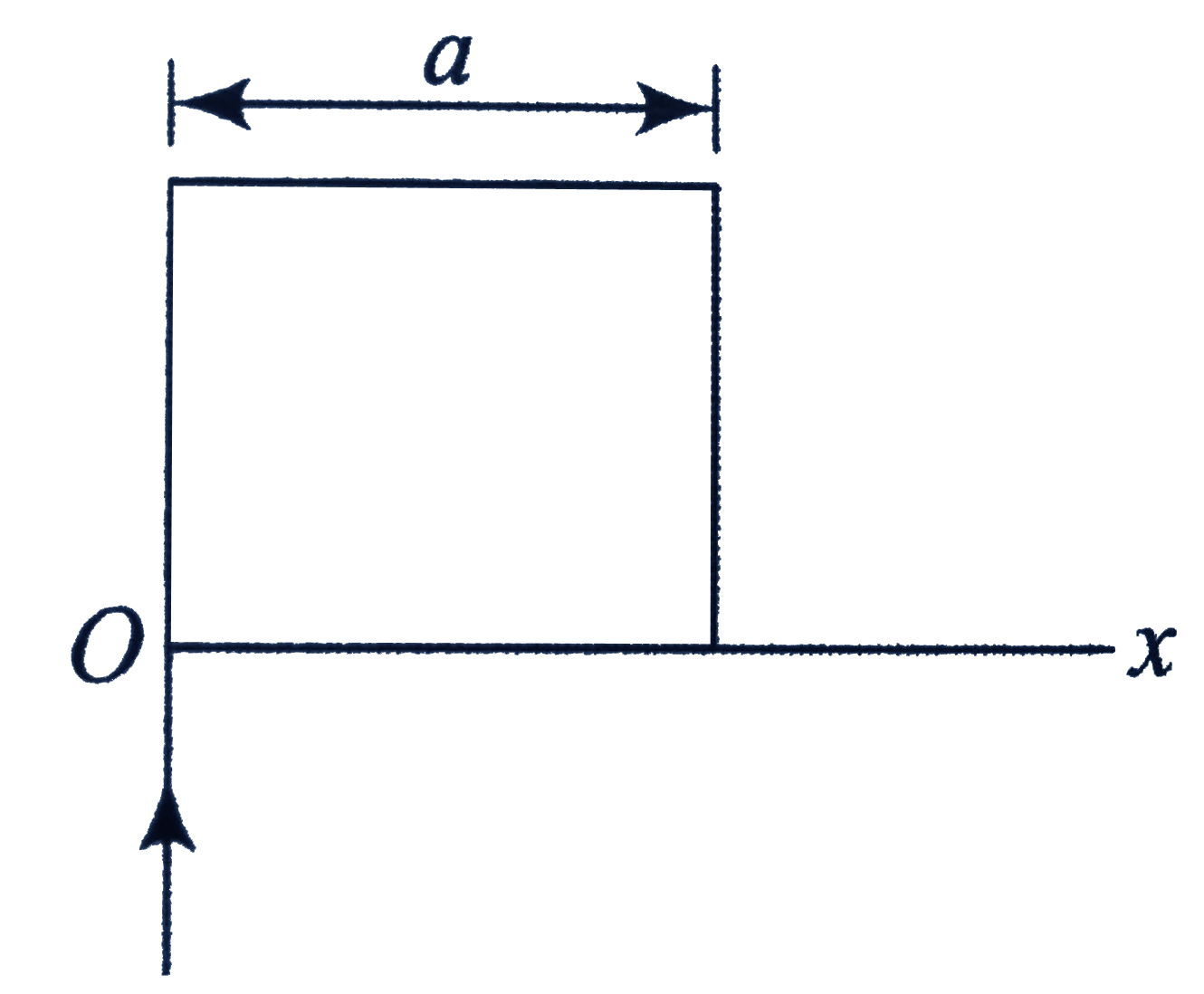
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionThe refractive index of glycerine is 1.46. What is the speed of light in air if its speed in glycerine is 2.05x108m/s ?
View Solution