Due to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as $n = n_{0}$ $\sqrt{1 + a y}$ , where $n_{0}$ is the index of refraction at the surface and $a = 2.0 \times 10^{- 6} m^{- 1}$ . A person of height $h = 2.0 m$ stands on a level surface. Beyond what distance will he not see the runway?
$Due to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n(0)sqrt(1+ay), where n(0) is the index of refraction at the surface and a=2.0xx10^(-6)m^(-1) . A person of height h=2.0 m stands on a level surface. Beyond what distance will he not see the runway?$

Text Solution

Verified by Experts

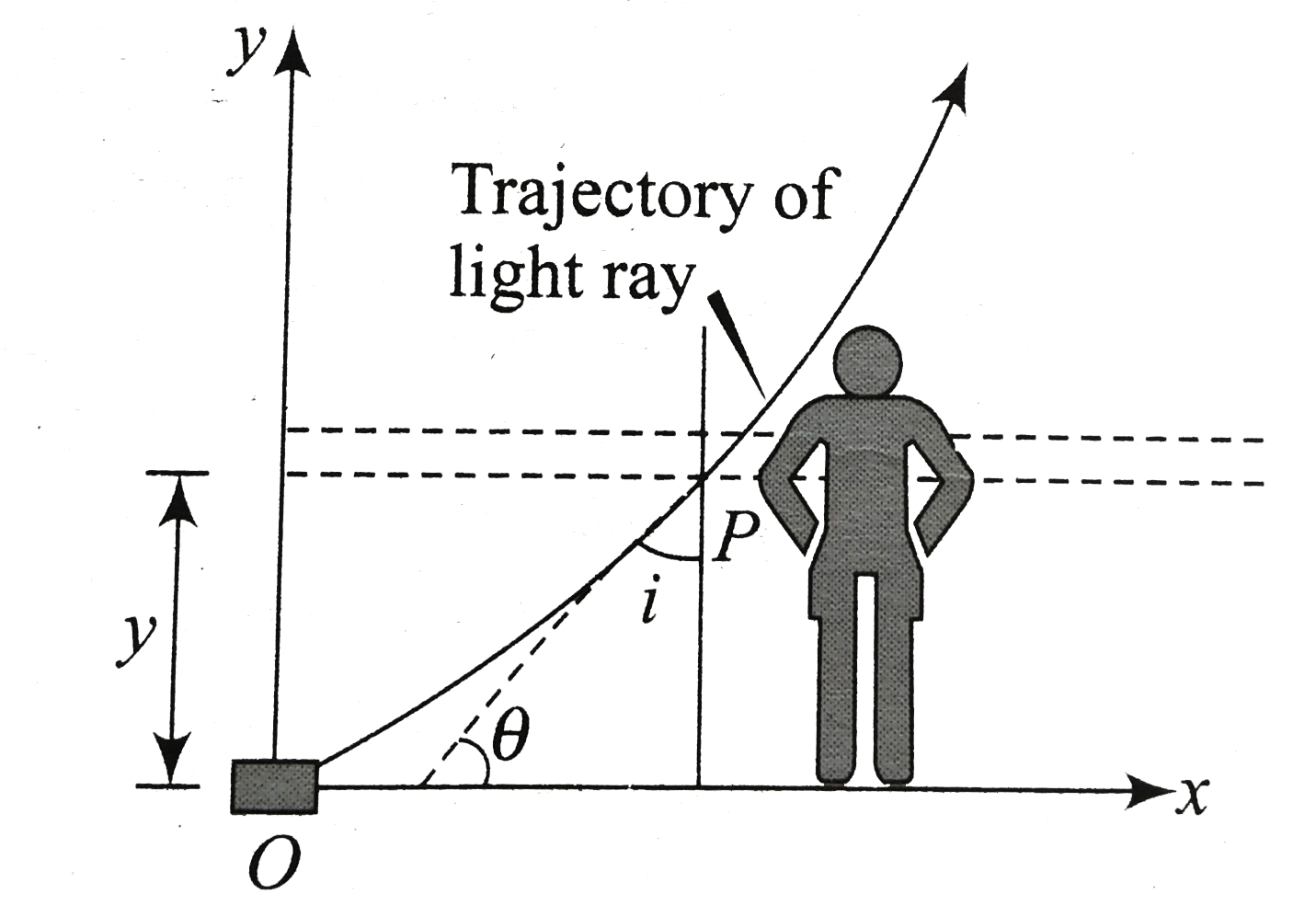
As refractive index is changing along y-direction, we can assum a number of thing layers of air placed parallel to x-axis. Let O be the distant object just visible to the man. Consider a layer of air at a distance y from the ground. Let P be a point on the trajectory of the ray. Form Fig. , $θ = 90^{\circ} - i$ .
The slope of trangent at point P is $tan θ = d y / d x = cot i$ .
From Snell's law, n sin i= constant
At the surface, $n = n_{0}$ and $i = 90^{\circ}$ .
$n_{0} {sin 90}^{\circ} = n sin i = (n_{0} \sqrt{1 + a y}) sin i$
$sin i = \frac{1}{\sqrt{1 + a y}} \Rightarrow cot i = \frac{d y}{d x} = \sqrt{a y}$
$\int_{0}^{y} \frac{d y}{\sqrt{a y}} = \int_{0}^{x} d x \Rightarrow x = 2 \sqrt{\frac{y}{a}}$
On substituting $y = 2.0 m$ and $a = 2 \times 10^{- 1}$ , we have
$x_{max} = 2 \sqrt{\frac{2}{2 \times 10^{- 6}}} = 2000 m$

Updated on:21/07/2023

A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as $μ = μ_{0} \sqrt{(1 + a y)}$ where $μ_{0}$ is the refractive index of air near the road and a= $2 \times 10^{- 6} / m$ . What is the actual length of the road, man is able to see
A2000m
B390m
Cinfinite distance
DNone of these
When a lens of refractive index $n_{1}$ is placed in a liquid of refractive index $n_{2}$ , the lens looks to be disappeared only if
A $n_{1} = \frac{n_{2}}{2}$
B $n_{1} = \frac{3}{4} n_{2}$
C $n_{1} = n_{2}$
D $n_{1} = \frac{5}{4} n_{2}$
A light ray enters into a medium whose refractive index varies along the x-axis as $n (x) = n_{0} \sqrt{1 + \frac{x}{4}}$ where $n_{0} = 1$ . The medium is bounded by the plates $x = 0, x = 1$ & $y = 0$ . It the ray enters at the origin at an angle $30^{\circ}$ with x-axis

Aequation of trajectory of the light ray is $y = [\sqrt{3 + x} - \sqrt{3}]$
Bequation of trajectory of the light ray is $y = 2 [\sqrt{3 + x} - \sqrt{3}]$
Cthe coordinate the point at which light ray comes out from the medium is $[1, 2 (2 - \sqrt{3})]$
Dthe coordinate the point at which light ray comes out from the medium is $[0, 2 (2 - \sqrt{3})]$