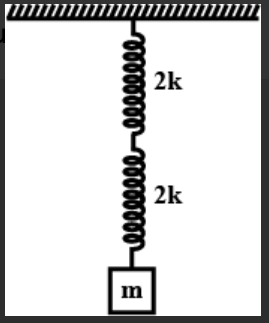
A system is shown in the figure. The force The time period for small oscillations of the two blocks will be

2π√3mk
2π√3m2k
2π√3m4k
2π√3m8k
The correct Answer is:C
Both the spring are in series
∴Keq=K(2K)K+2K=2K3
Time period T=2π√μKeq
where μ=m1m2m1+m2 Here μ=m2
∴T=2π√m2.32K=2π√μKeq
OR
_E01_018_S01.png)
Total extensin =2x
By energy conservation
E=12Keq(2x)2+12mv2+12mv2
E=122k34x2+12mv2+12mv2=43kx2+mv2
dEdt=43k(2x)dxdt+m(2v)dvdt
there is no loss of energy
dEdt=0⇒83kxv+2mva=0⇒8kxv3=−2mva
a=−4kx3m⇒−ω2x=−4kkx3m⇒ω=√4k3m
T=2πω⇒2π√3m4k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Knowledge Check
A system is shown in the figure. The force The time period for small oscilations of the two blocks will be
 A2π√3mKB2π√3m2KC2π√3m4KD2π√3m8K
A2π√3mKB2π√3m2KC2π√3m4KD2π√3m8KThe time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
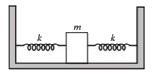 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k
Find time period of oscillation of the system.

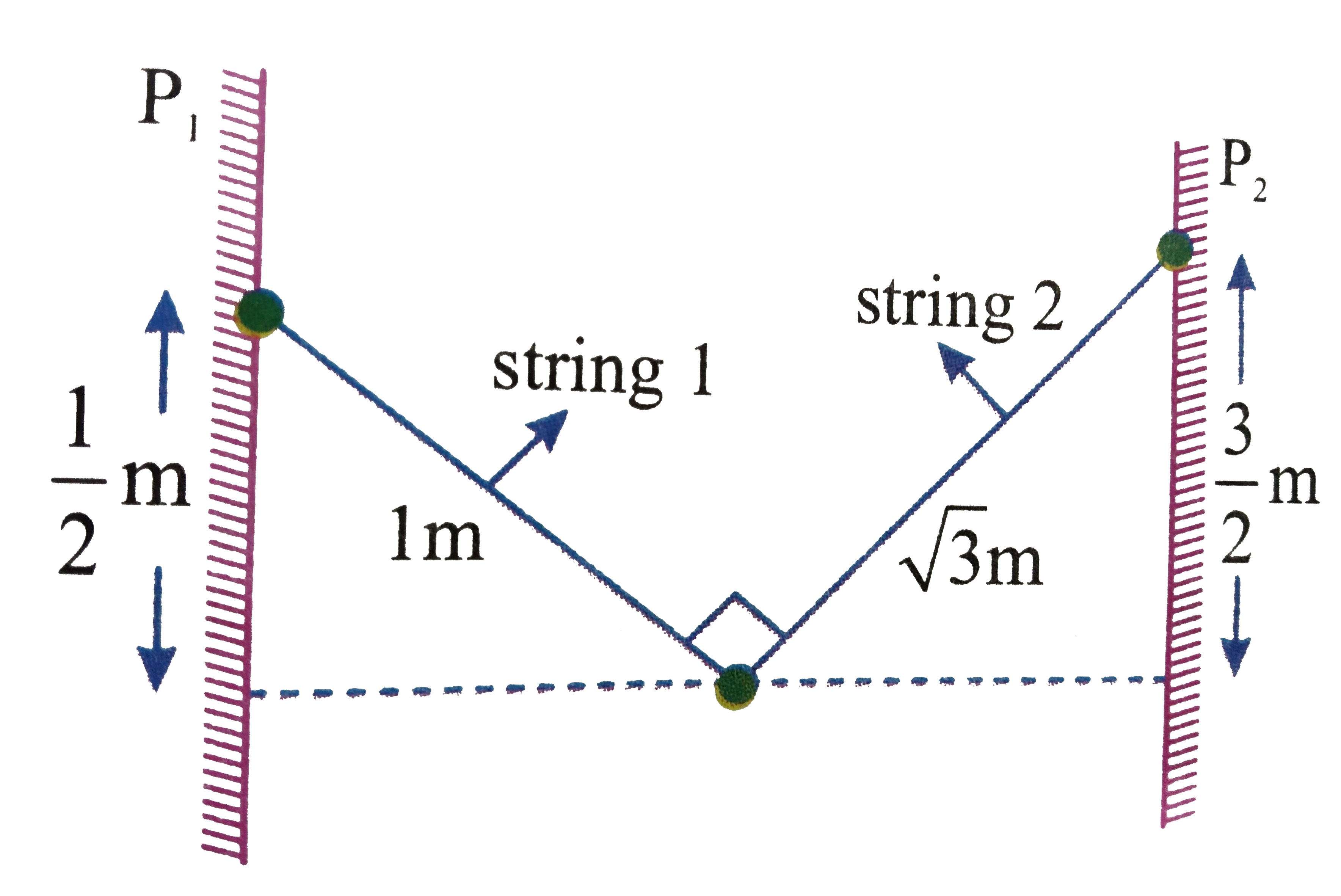
View SolutionA small particle is tied by the help of two strings to vertical walls with the parameters as shown in the figure (g=π2). The time period of the small oscillations of the particle if it is displaced perpendicular to the plane of the paper slightly is x sec, the value of x is ____________
View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
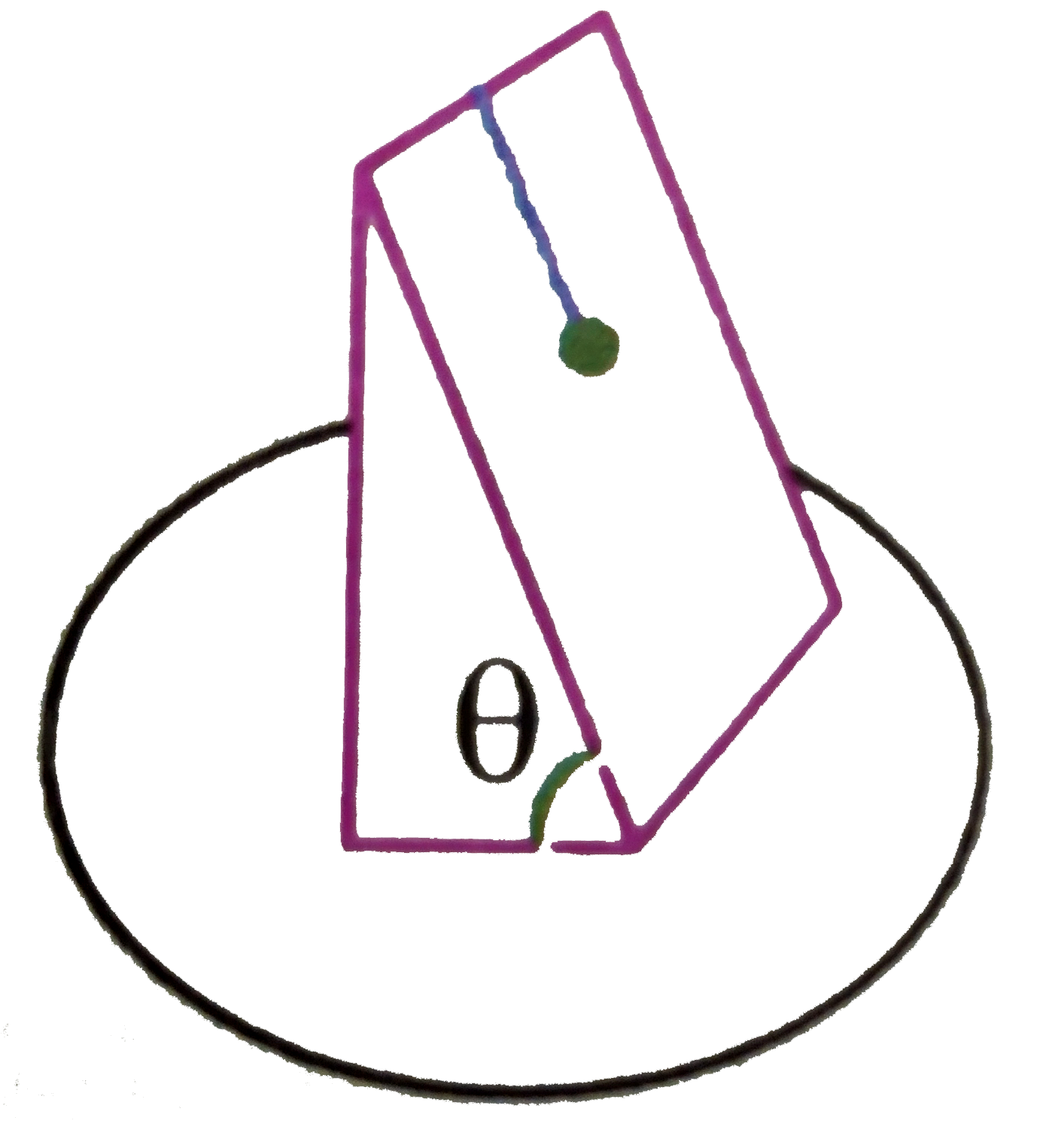
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View Solution