A solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
2π√Mk
2π√3m2k
2π√M2k
2π√2M3k
The correct Answer is:B
Let small angular displacement of cylinder be θ then restoring torque
Iα=−k(Rθ)R where I=32MR2
⇒d2θdt2+kR232MR2θ=0⇒d2θdt2+2k3Mθ=0⇒ω2=2k3m
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason7videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.
 View Solution
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
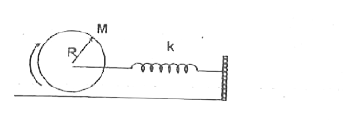 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπ - Question 2 - Select One
A solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is
 A2π√xgB2π√2M3KC2π√3M8KD2π√3M2K
A2π√xgB2π√2M3KC2π√3M8KD2π√3M2K - Question 3 - Select One
A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
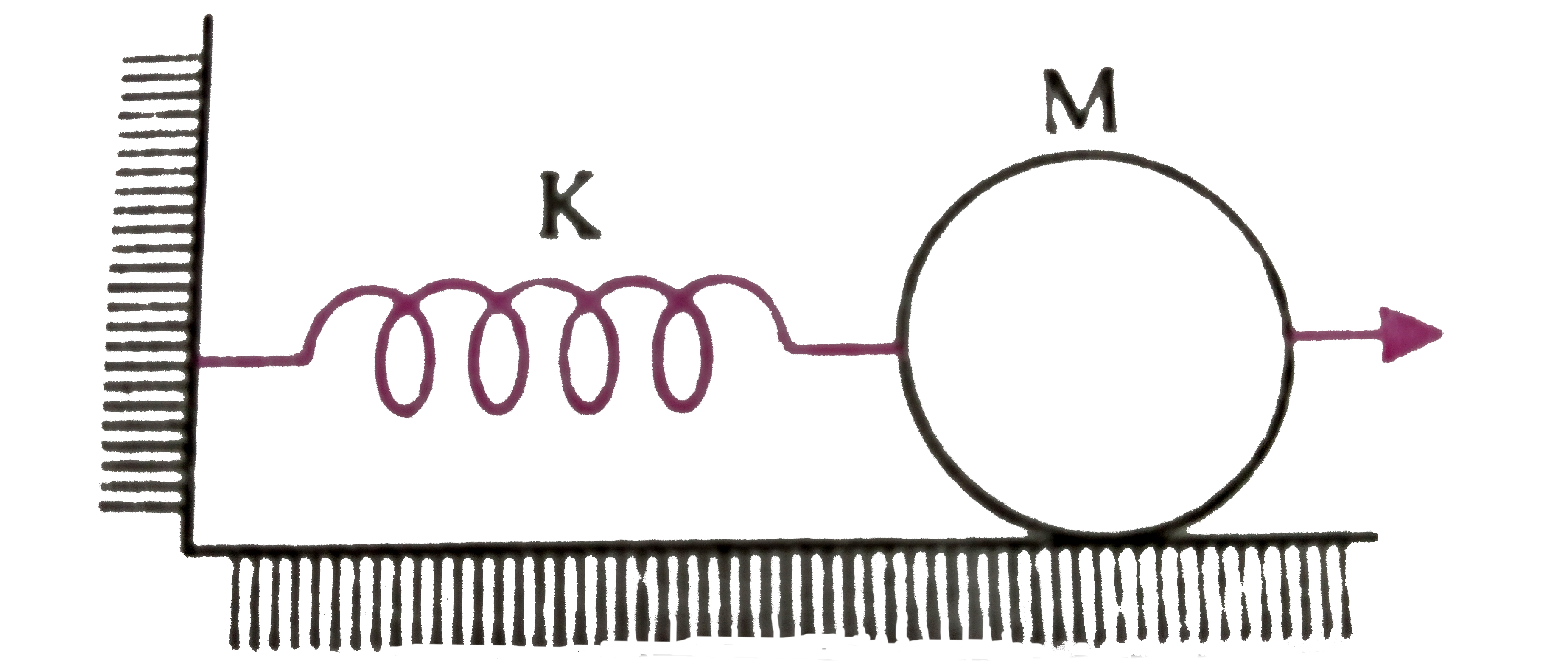 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
 View Solution
View SolutionA solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.
 View Solution
View SolutionOn an uniform cylinder of mass m and radius R a constant horizontal force F is applied at any point. Choose the correct alternative if cylinder is rolling without slipping in rightward direction
 View Solution
View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is
 View Solution
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solution

