A half ring of mass m, radius R is hanged at its one end its one end in verical plane and if free to socilalte in its plane.
Find oscillations frequency of the half ring.
_E01_109_Q01.png)
The correct Answer is:A, B, D
Moment of inertia about hinged point
I=mR2+mR2=2mR2
f=12π√mglI=12π
⎷mg√R2+4R2π22mR
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
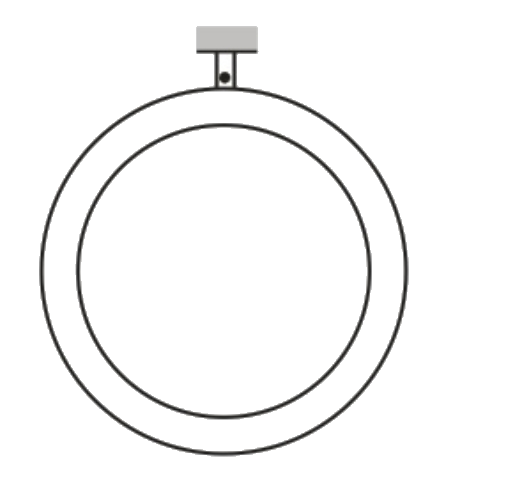 View Solution
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View Solution
Knowledge Check
- Question 1 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 2 - Select One
A uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√2RgBπ√2RgCπ2√RgDπ√R2g - Question 3 - Select One
A uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√rgB2pi sqrt((5 R)/(3 g))C2π√7R5gD2π√2R5g
A hemispherical sheli of mass M and radius R made to vibrate as shown in figure. Find its frequency of oscillation.
 View Solution
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
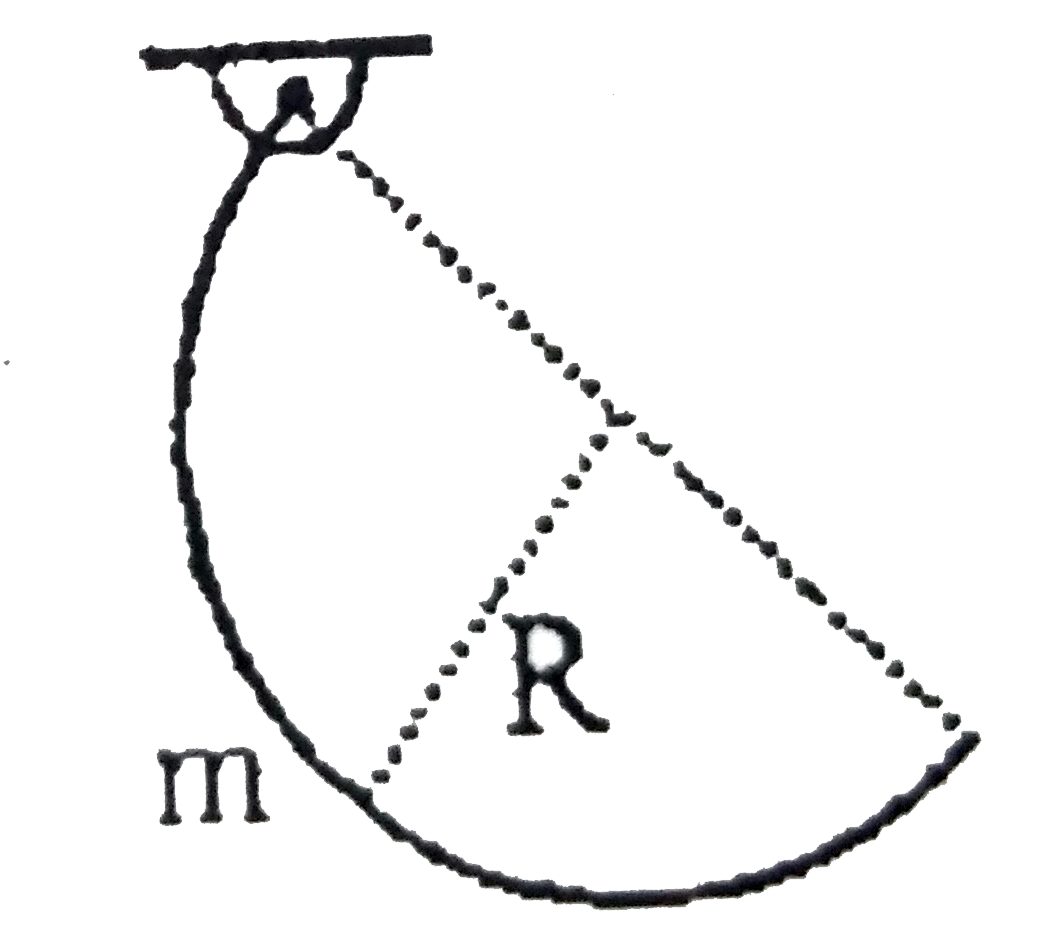 View Solution
View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View SolutionThe M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View Solution

