Two identical rods each of mass $m$ and length $L$ , are tigidly joined and then suspended in a vertical plane so as to oscillate freely about an axis normal to the plane of paper passing through $' S'$ (point of supension). Find the time period of such small oscillations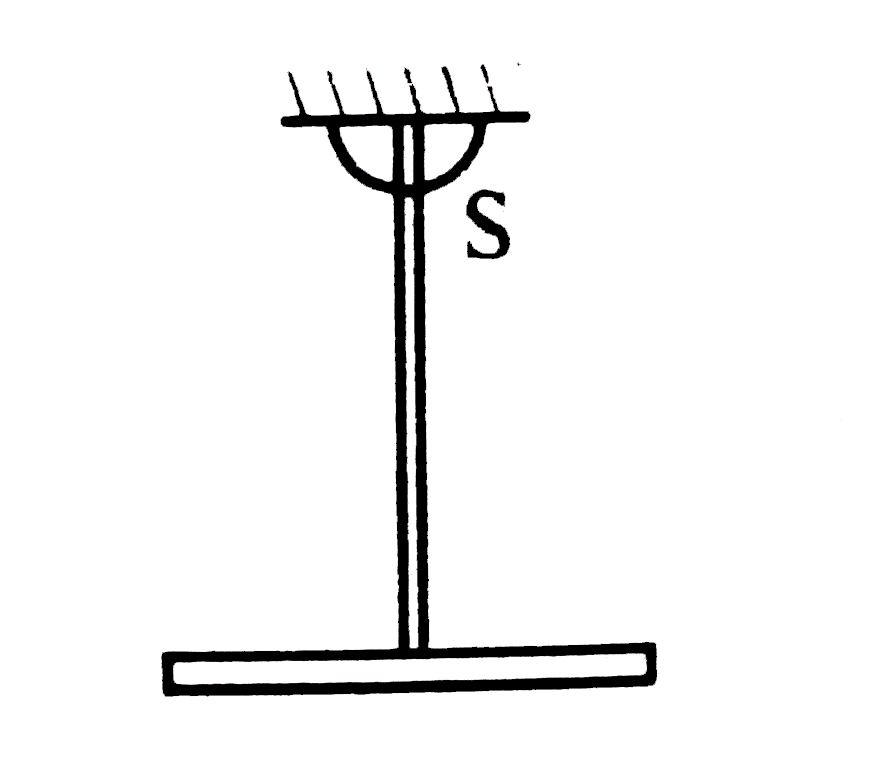

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

$T = 2 π \sqrt{\frac{I}{m g l}}$ where
$I = \frac{m L^{3}}{3} + (\frac{m L^{2}}{12} + m L^{2})$
$= \frac{17 m L^{2}}{12}$ & $l = \frac{3 L}{4}$
(Distance of centre of mass form hinge)
$\Rightarrow T = 2 π \sqrt{\frac{17 m L^{2}}{12 (2 m g (3 L / 4))}} = 2 π \sqrt{\frac{17 L}{18 g}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.

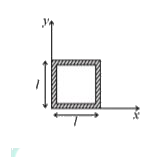A $\frac{5}{3} m l^{2}$
B $\frac{4}{3} m l^{2}$
C $m l^{2}$
DNone of these
Question 2 - Select One
Two identacal rods each of length $l$ and mass $m$ weided toeather at right angle and edge suspended from a kinetic sides as shown Angular frequency of small oscillation of the system in its then plane about the total of suspension is

A $\sqrt{\frac{3 g}{4 \sqrt{2} l}}$
B $\sqrt{\frac{3 g}{2 \sqrt{2} l}}$
C $\sqrt{\frac{3 g}{\sqrt{2} l}}$
DNone of these
Question 3 - Select One
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

A $2 π \sqrt{\frac{l}{g}}$
B $2 π \sqrt{\frac{2 l}{g}}$
C $2 π \sqrt{\frac{2 l}{3 g}}$
D $2 π \sqrt{\frac{l}{3 g}}$

ALLEN-SIMPLE HARMONIC MOTION-Exercise-04 [A]

Home
Ask Doubt
Profile