In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end. Rotational SHM of the rod (Mass m, length L) will occur only if-
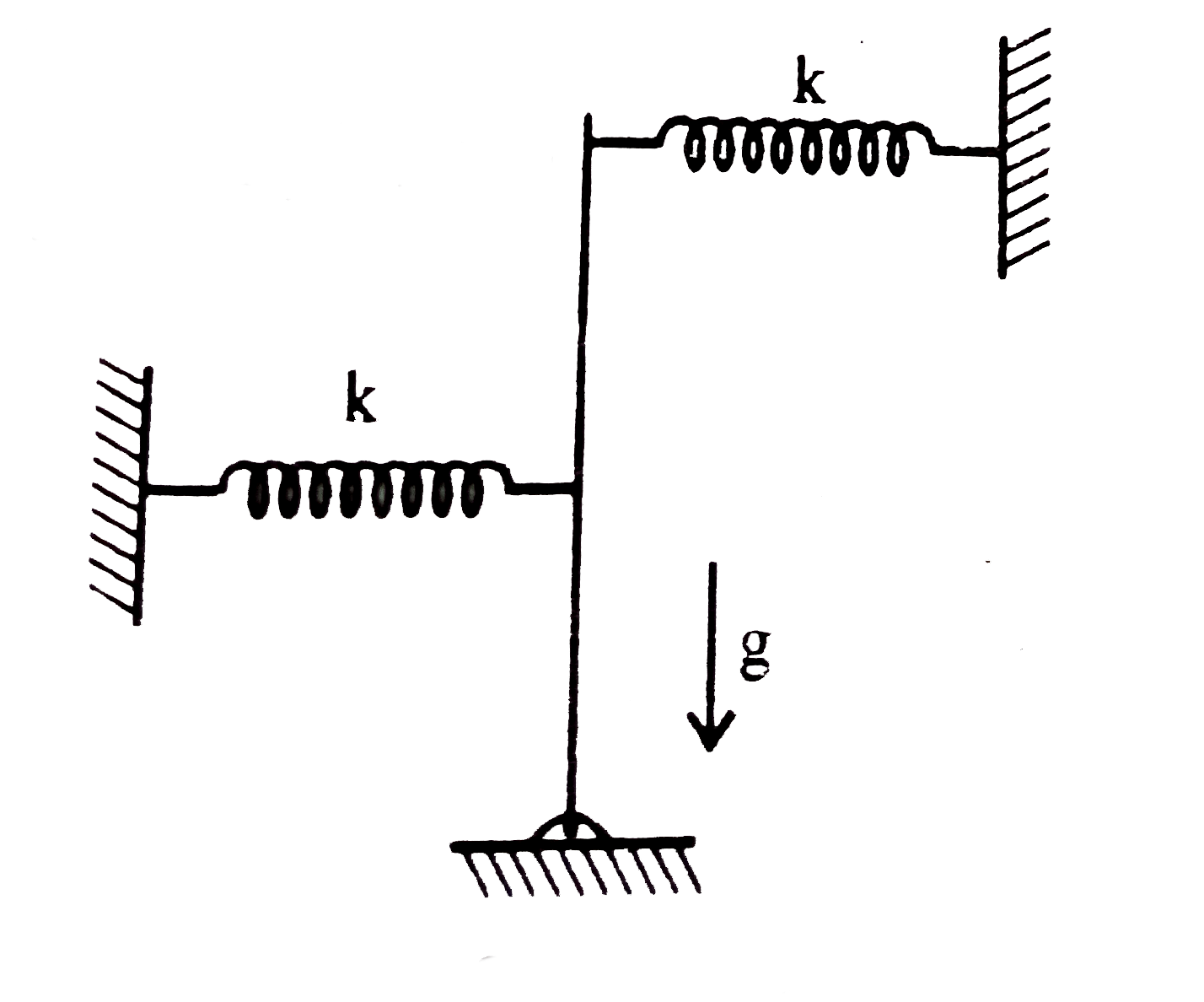
The correct Answer is:B, C
_E01_118_S01.png)
θ=x1l/2,x1=θl2,f1=Kθl2
θ=x2l,x2=θl,l2=kθl
τ=L2×F1+L×F2≥mgsinθL2
⇒L2KθL2+LKθL≥m>hηL2
⇒54KθL2≥mgθl2⇒K≥2mg5L
(ii) If the rod is displacement through an angle θ, then
−(kLθ)L−(kL2θ)L2+Mg(L2)θ=ML23α(k=MgL)
⇒9kθ4M=α⇒ω32√km
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05(B)46videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s8videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 04[A]25videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Figure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rodView Solution
Knowledge Check
- Question 1 - Select One
In the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of these - Question 2 - Select One
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lg - Question 3 - Select One
A rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
Ais simple harmonicBis oscillatory but not simple harmonicCis pericolic but not oscillatoryDmay be simple harmonic
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
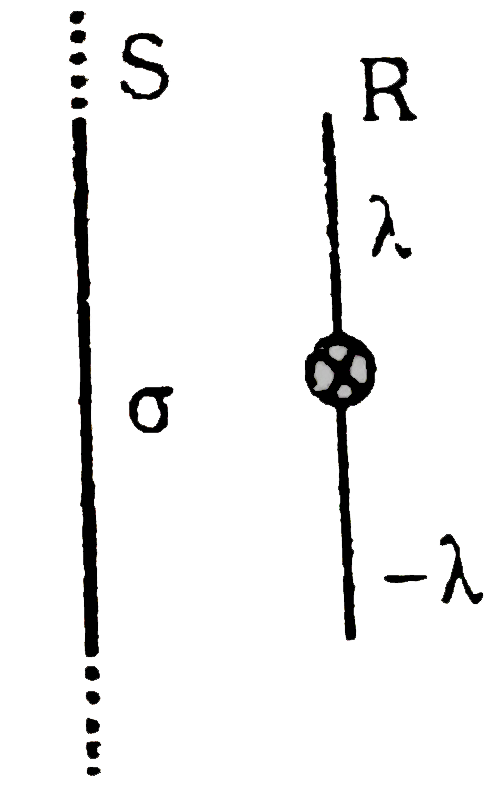 View Solution
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionUniform rod Ab is hinged at the end A in the figure. The other end of the rod is connected toa block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are
 View Solution
View Solution

