A rod of mass M and length K is hinged at its one end n carris a block f mass m at its other end. A spring of force constant k1 is installed at distance a form the hinge and another of force constant k2 at a distance b as shown in the figure. If the whole arrangement rests on a smoth horizontal table top. Find the frequency of vibrations.
_E01_120_Q01.png)
The correct Answer is:A, B, C
_E01_120_S01.png)
For small angular displacement θ, net torque towards mean position is
τ=(k1aθ)a+(k2bθ)b⇒Iα=(k1a2+K2b2)θ
⇒(mL2+13ML2)α=(k1a2+k2b2)θ
⇒α=k1a2+k2b2L2(m+M3)θ∴ω2=k1a2+k2b2L2(m+M3)
Hence frequency
f=ω2π=12π
⎷k1a2−k2b2L2(m+M3)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05(B)46videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s8videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 04[A]25videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
View SolutionFind the frequency of oscillations of the system in the figure. The bar is rigid and light.
[Hint: A spring of force constant k1 at a distance a is equivalent to a spring of force constant k1(ab)o2 at a distance b)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k1 is installed at distance a from the hinge and another of force constant k2 at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
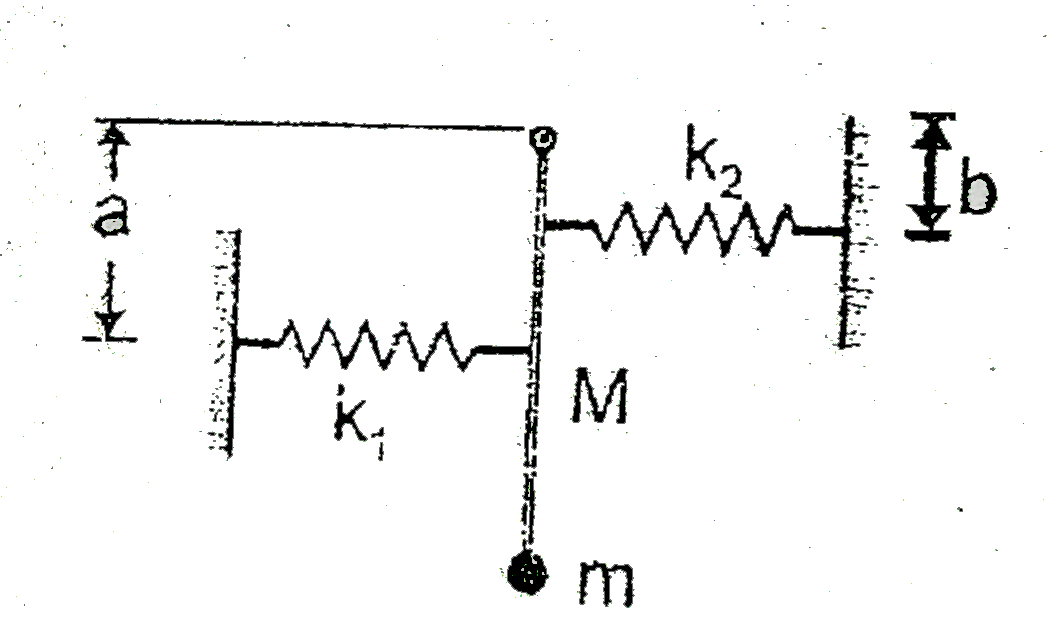 A12π ⎷k1a2+k2b2L2(m+M3)B12π√k2+k1M+mC12π ⎷k2+k1a2b24M3+mD12π ⎷k1+k2b2a243m+M
A12π ⎷k1a2+k2b2L2(m+M3)B12π√k2+k1M+mC12π ⎷k2+k1a2b24M3+mD12π ⎷k1+k2b2a243m+M - Question 2 - Select One
A rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k1 is installed at distance a from the hinge and another of force constant k2 at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
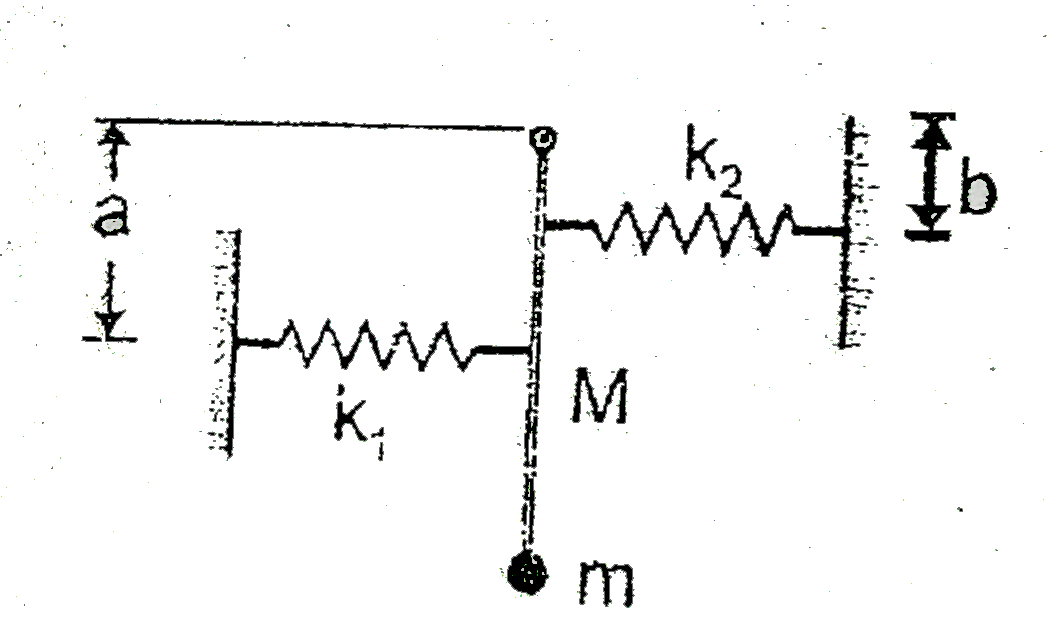 A12π ⎷k1a2+k2b2L2(m+M3)B12π√k2+k1M+mC12π ⎷k2+k1a2b24M3+mD12π ⎷k1+k2b2a243m+M
A12π ⎷k1a2+k2b2L2(m+M3)B12π√k2+k1M+mC12π ⎷k2+k1a2b24M3+mD12π ⎷k1+k2b2a243m+M - Question 3 - Select One
A rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
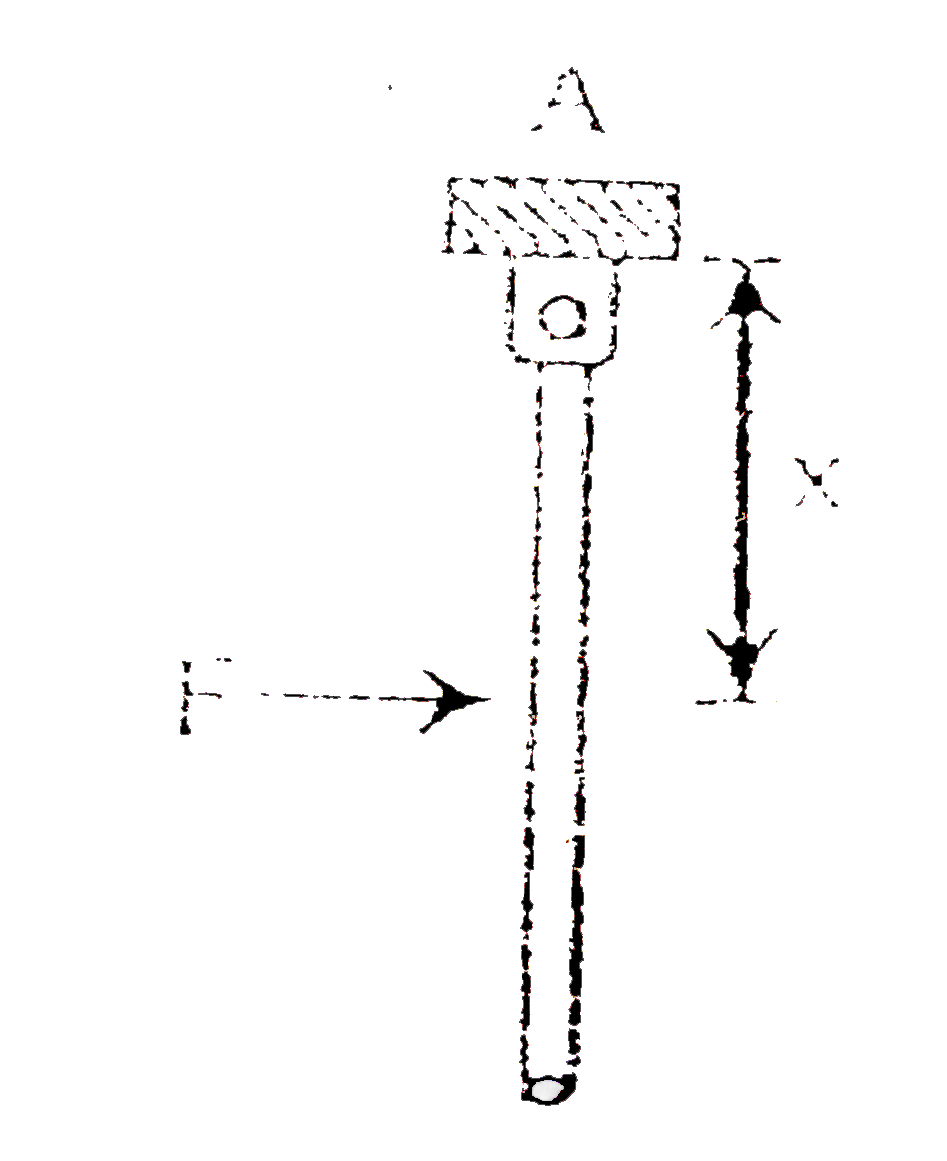 A
A B
B C
C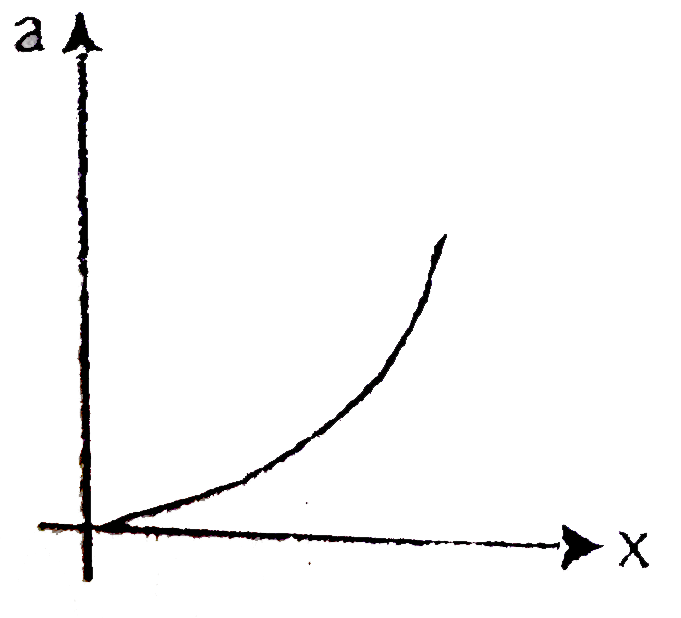 D
D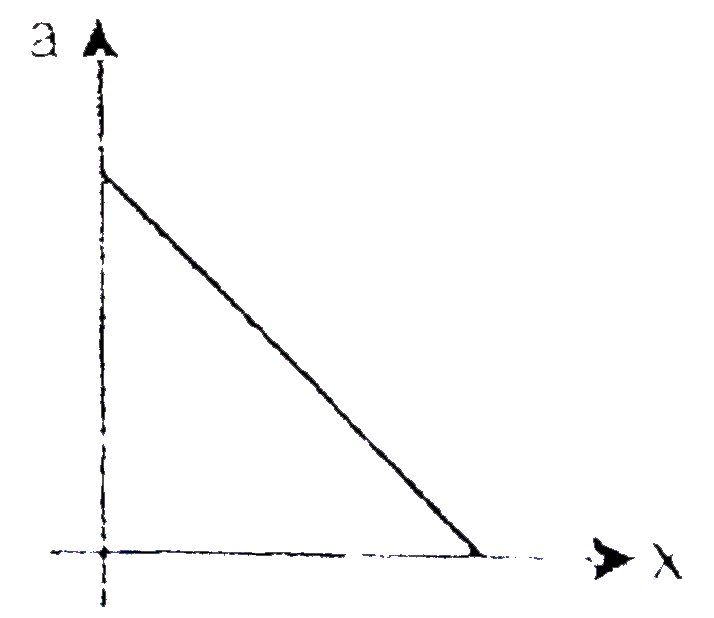
A rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass (a) variea with x as:
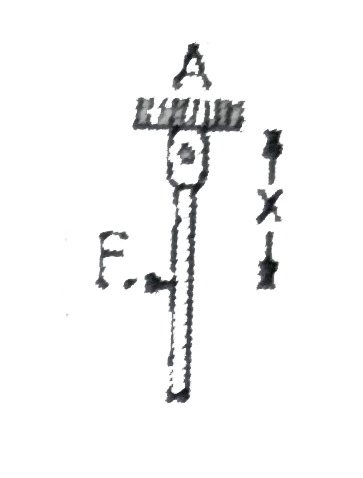 View Solution
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as
 View Solution
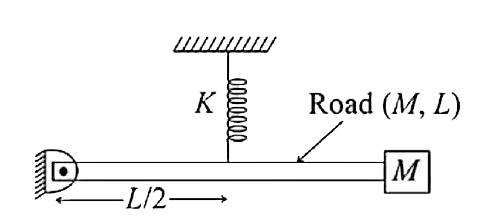
View SolutionA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
 View Solution
View SolutionA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 View Solution
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 View Solution
View Solution

