Two masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
The correct Answer is:(i) v0t+Am1m2(1−cosωt) , (ii) (m1m2+1)A
(i) Two massse m1 and m2 are connected by a spring of length l0. The spring is in compressed position. It is held in this position by a string. When the string snaps, the spring force is brought into operation. The spring force is an internal force w.r.t masses-spring system. No external force is applied on the system. The velocity of centre of mass will not change.
Velocity of centre of mass =v0
∴ Location/x -coordinate of centre of mass of time
t=v0t
∴¯v=m1x1+m2x2m1+m2
⇒v0t=m1[v0t−A(1−cosωt)]+m2x2m1+m2
⇒(m1+m2)v0t=m1[v0t−A(1−cosωt)]+m2x2)
⇒m1v0t+m2v0t=m1v.0t−m1A(1−cosωt)]+m2x2
⇒m2x2=m2v0t+m1A(1−cosωt)
⇒x2=v0t+m1Am2(1−cosωt)......(i)
To express l0 in terms of A.
∴x1=v0t−A(1−cosωt)∴dx1dt2=−Aω2sinωt
∴d2x2dt2=−Aω2cosωt........(ii)
x1 is displacement of m1 at time t.
∴d2x1dt2= acceleration of m1 at time t.
When the spring attains its natural length l0, then acceleration is zero and (x2−x1)=l0)
∴x2x1=l0 , Put x2 from (i)
⇒[v0t+m1Am2(1−cosωt)]−[v0t−A(1−cosωt)]=l0
⇒l0=(m1m2+1)A(1−cosωt)
When d2x1dt2=0,cosωt=0 from (ii).
∴l0=(m1m2+1)A.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Solved Example
Explore 3 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:X Rays : Solved Example
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Paragraph
Explore 3 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Two masses m1 and m2 connected by a light spring of natural length l0 is compressed completely and tied by a string. This system while moving with a velocity v0 along +vex-axis pass through the origin at t=0. At this position the string snaps. Postion of mass m1 at time t is given by the equation. x1(t)=v0t−A(1−cosωt) calculate :
(a) Position of the particle m2 as a function of time.
(b) l0 in terms of A.
View SolutionTwo point masses m1 and m2 are connected by a spring of natural length l0. The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity v0 along positive x-axis. When the system reached the origin, the string breaks (t=0). The position of the point mass m1 is given by x1=v0t−A(1−cosωt) where A and ω are constants. Find the position of the second block as a function of time. Also, find the relation between A and l0.
View Solution
Knowledge Check
vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
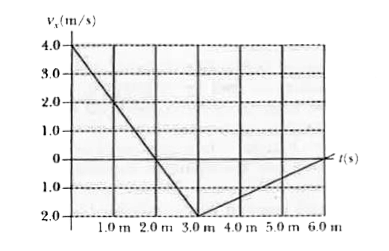 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 mVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0m
Two point masses m1 and m2 are connected by a spring of natural length l0. The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity v0 along positive x-axis. When the system reached the origin, the string breaks (t=0). The position of the point mass m1 is given by x1=v0t−A(1−cosωt) where A and ω are constants. Find the position of the second block as a function of time. Also, find the relation between A and l0.
View SolutionThe position of a particle at time t is given by the equation x(t)=V0A(1−eAt)
V0 = constant and A > 0
Dimensions of V0 and A respectively are
View SolutionThe position of a particle at time t, is given by the equation, x(t)=v0α(1−e−αt), where v0 is a constant and α>0. The dimensions of v0 & α are respectively.
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View Solution
