A mass m is undergoing SHM in the verticl direction about the mean position y0 with amplitude A and anglular frequency ω. At a distance y form the mean position, the mass detached from the spring. Assume that th spring contracts and does not obstruct the motion of m. Find the distance y. (measured from the mean position). such that height h attained by the block is maximum (Aω2>g).
_E01_175_Q01.png)
The correct Answer is:mgk=gω2<a
A small body of mass attached to one end of a vertically hanging spring performs SHM.
Angular frequency =ω
Amplitude =a
Under SHM, velocity
v=ω√a20−y2
After detaching from spring net downward accelration of the block =g.
∴ Height attained by the block =h
∴h=y+v22g⇒h=y+ω2(a2−y2)2g
For h tq be maximum
dhdy=0,y=y∗
∴dhdy=1+ω22g(−2y∗)⇒0=1−2ω2y∗2g
⇒ω2y∗g=1⇒y∗=gω2
Since aω2>g (given)
∴a>gω2∴a>y∗.y∗
from mean position <a
Hence y∗=gω2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - X Rays : Solved Example2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
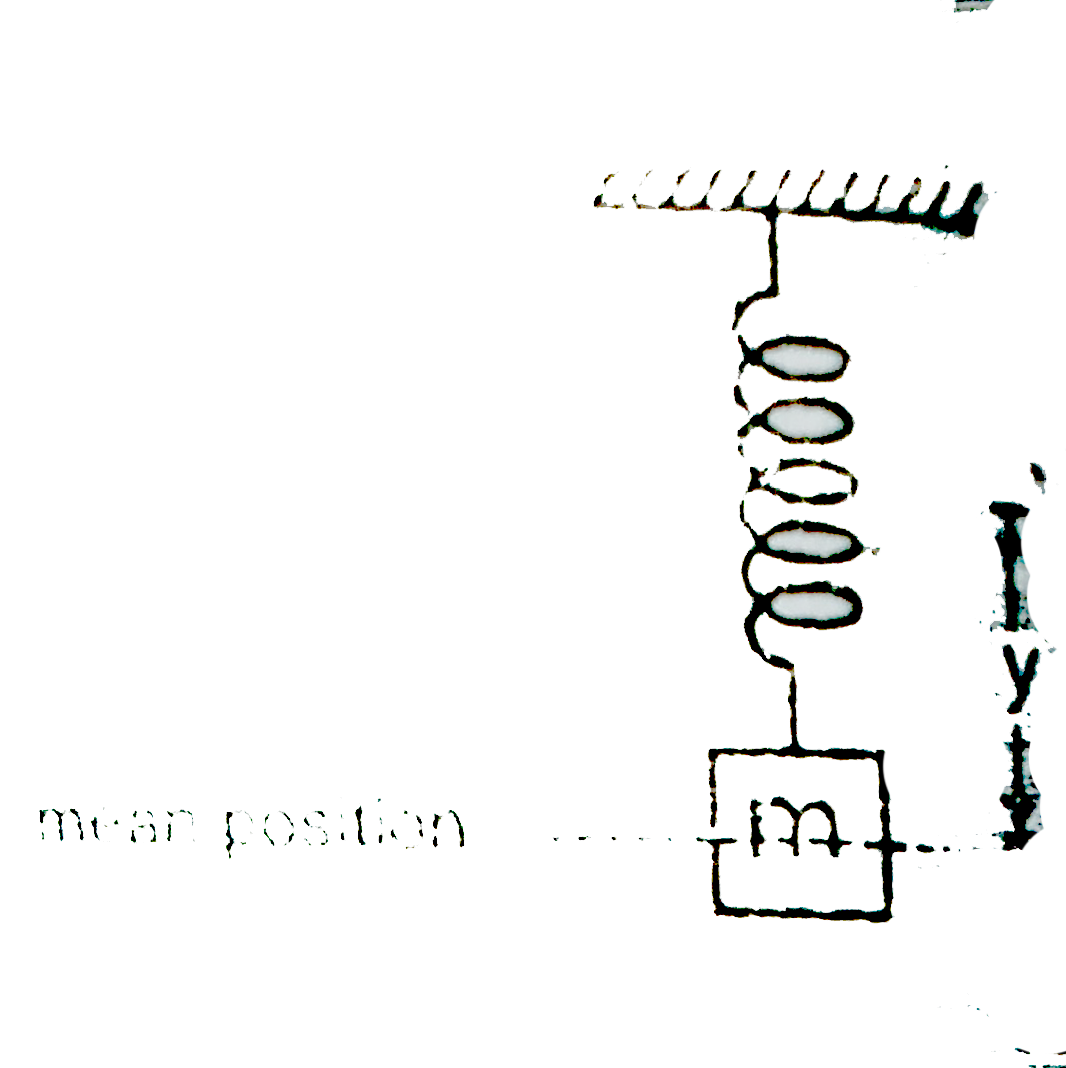 View Solution
View SolutionA block is performin SHM of amplitude 'A' in vertical direction. When block i8s at 'y' (measured from mean position), it detaches froms spring, so that spring contracts and does not effect the motion of the block. Find 'y⋅' such that block attains maximum height from the mean position. (given Aω2>g)
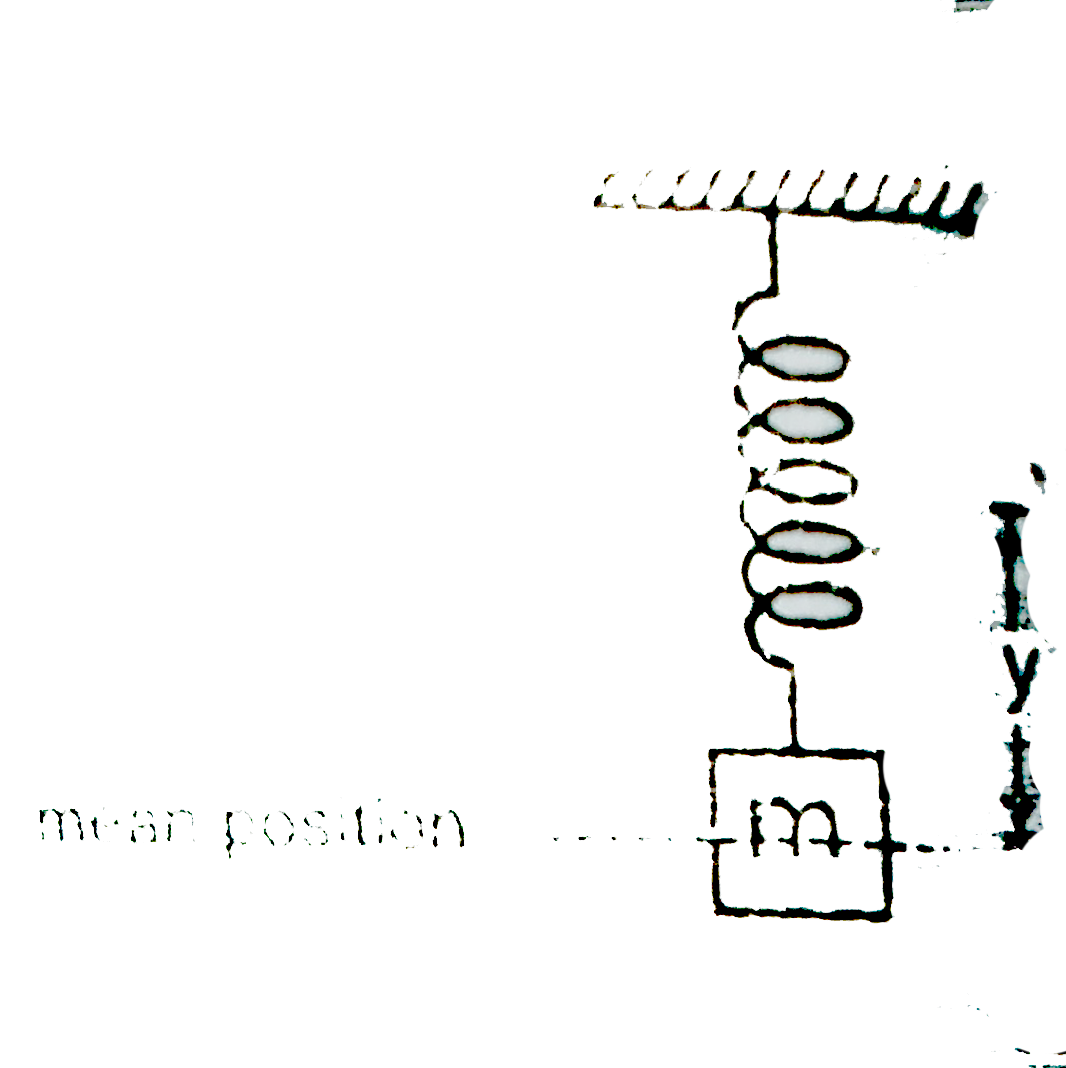 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The particle performing S.H.M. along a straight line about the mean position with an amplitude 'A'. Then the maximum potential energy at a distance A from the extreme position is
AAB0CA/2D(3/2)A - Question 2 - Select One
The particle performing S.H.M., about mean position it has
Amaximum acceleration and maximum velocityBminimum acceleration and maximum velocityCmaximum acceleration and minimum velocityDminimum acceleration and minimum velocity - Question 3 - Select One
The value of phase at maximum distance from the mean position of a particle in S.H.M. is :
Aπ/2BπCZeroD2π
A particle executes SHM with amplitude A and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.
View SolutionIn a S.H.M. with amplitude 'A', what is the ratio of K.E. and P.E. at A2 distance from the mean position ?
View SolutionThe velocity of a particle in simple harmonic motion at displacement y from mean position is
View SolutionA particle executes SHM of amplitude A. At what distance from the mean position is its KE equal to its PE ?
View SolutionThe amplitude and the periodic time of a S.H.M. are 5 cm and 6 sec respectively. At a distance of 2.5 cm away from the mean position, the phase will be
View Solution

