Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
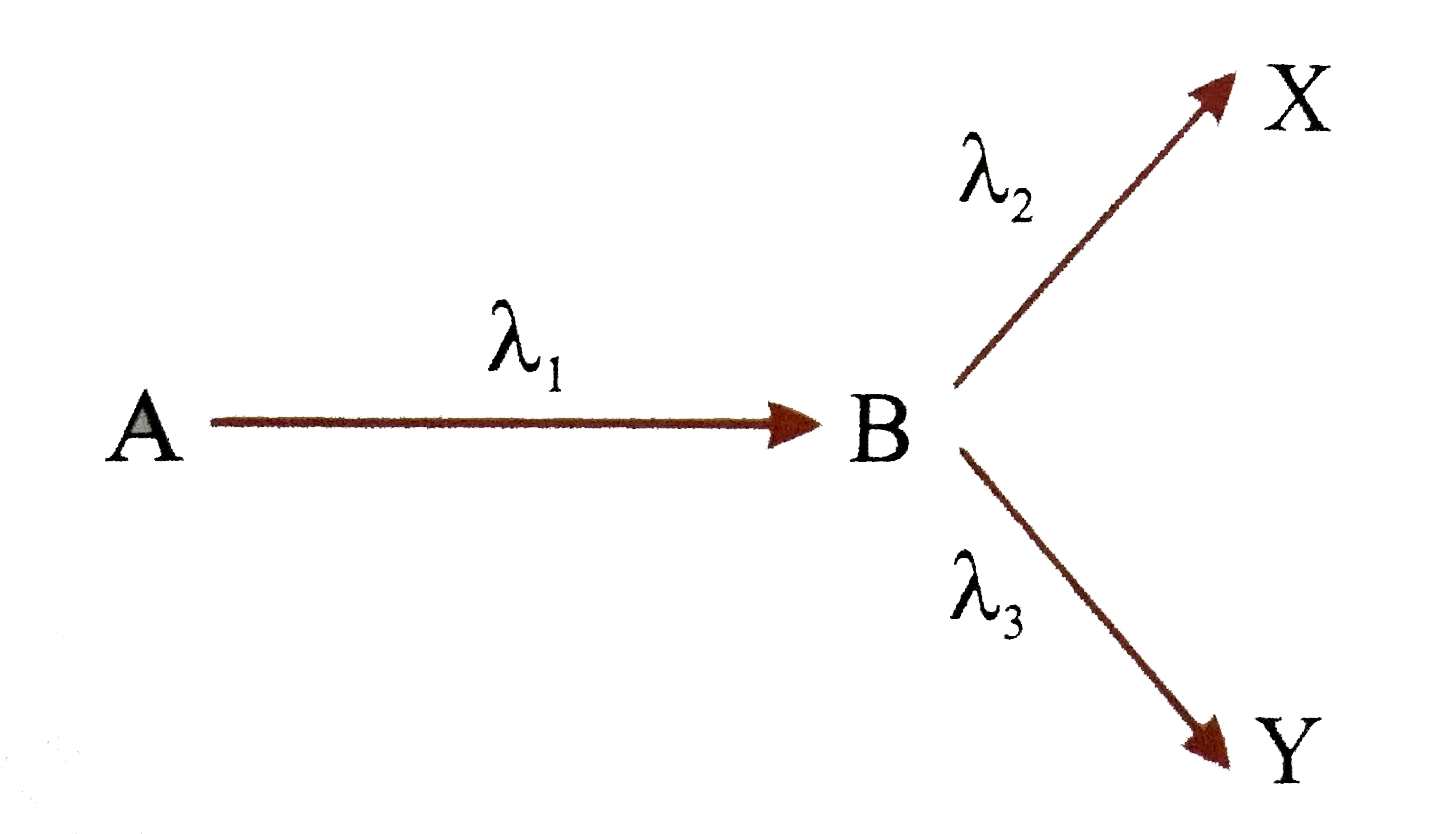
The net rate of accumulation of B at any instant is
N1λ1+N2λ2+N3λ3
N1λ1−N3λ2−N4λ3
N1λ1−N2λ2−N2λ3
N1λ1+N2λ2−N3λ3
The correct Answer is:C
Rate of production of B depends on the decaying rate (A) : dNAdt=−λNA=λN1
B is decaying simultaneously with two rates dNBdt=−λ2NB=−λ2N2
dNBdt=−λ3NB=−λ3N2
Number of nuclei of 'B' is =λ1N1−λ2N2−λ3N2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 372videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 382videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 342videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
The rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
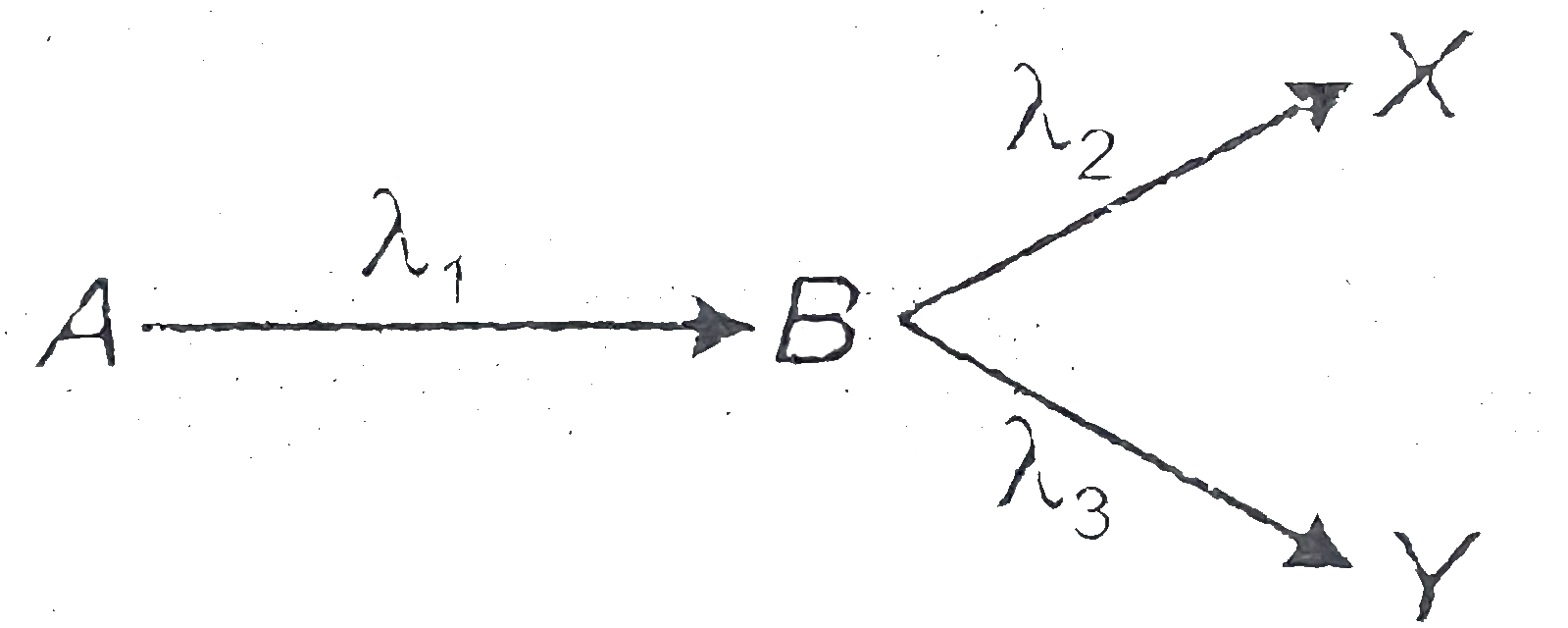
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
Rate of accumulation of B of any instant will beView SolutionThe rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively

and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
At t=∞, which of the following is incorrect ?View Solution
Knowledge Check
- Question 1 - Select One
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
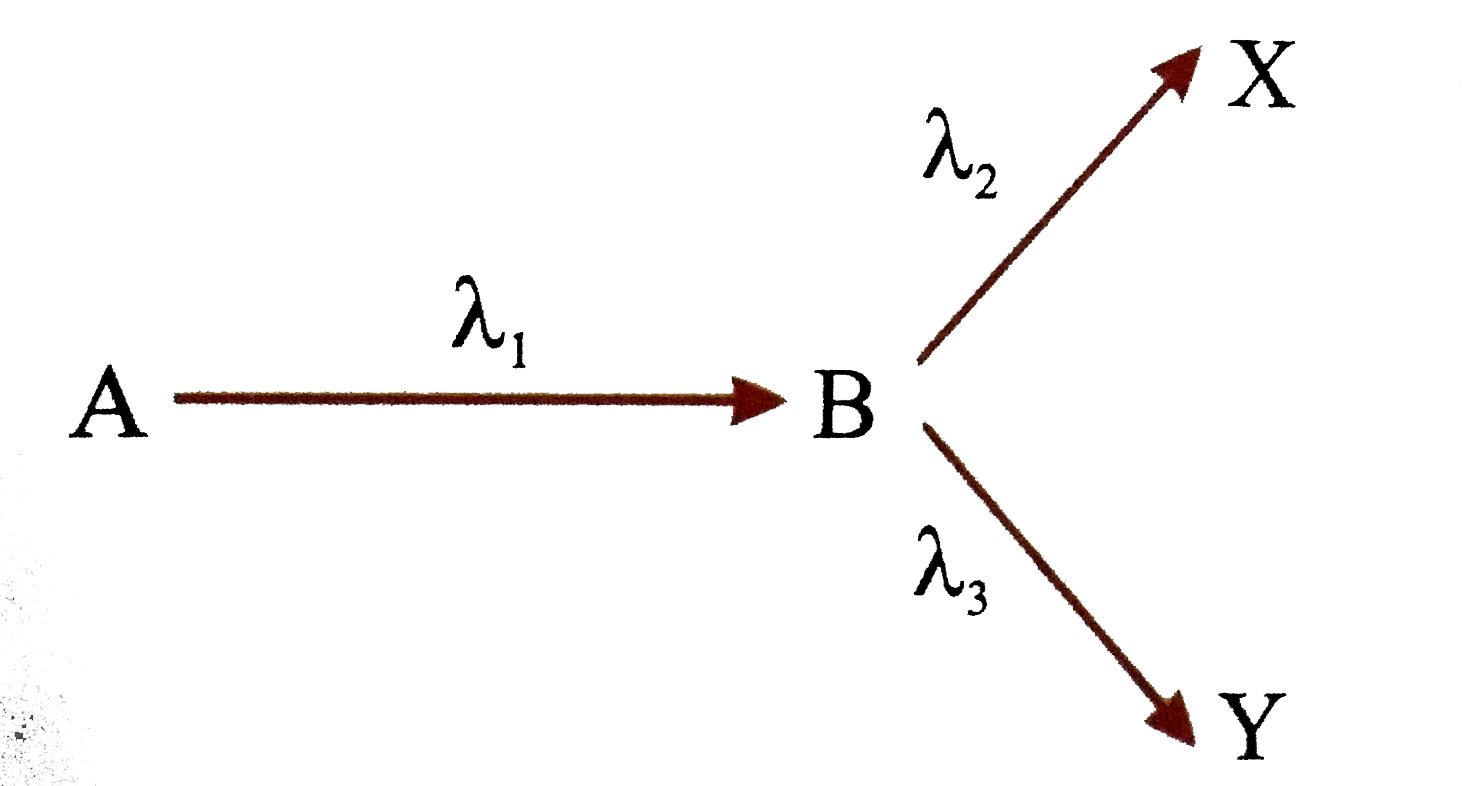
At t=∞, which of following is incorrect ?AN2=0BN3=N0λ2λ2+λ3CN4=2N0λ3λ2+λ3DN1+N2+N3+N4=2N0 - Question 2 - Select One
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
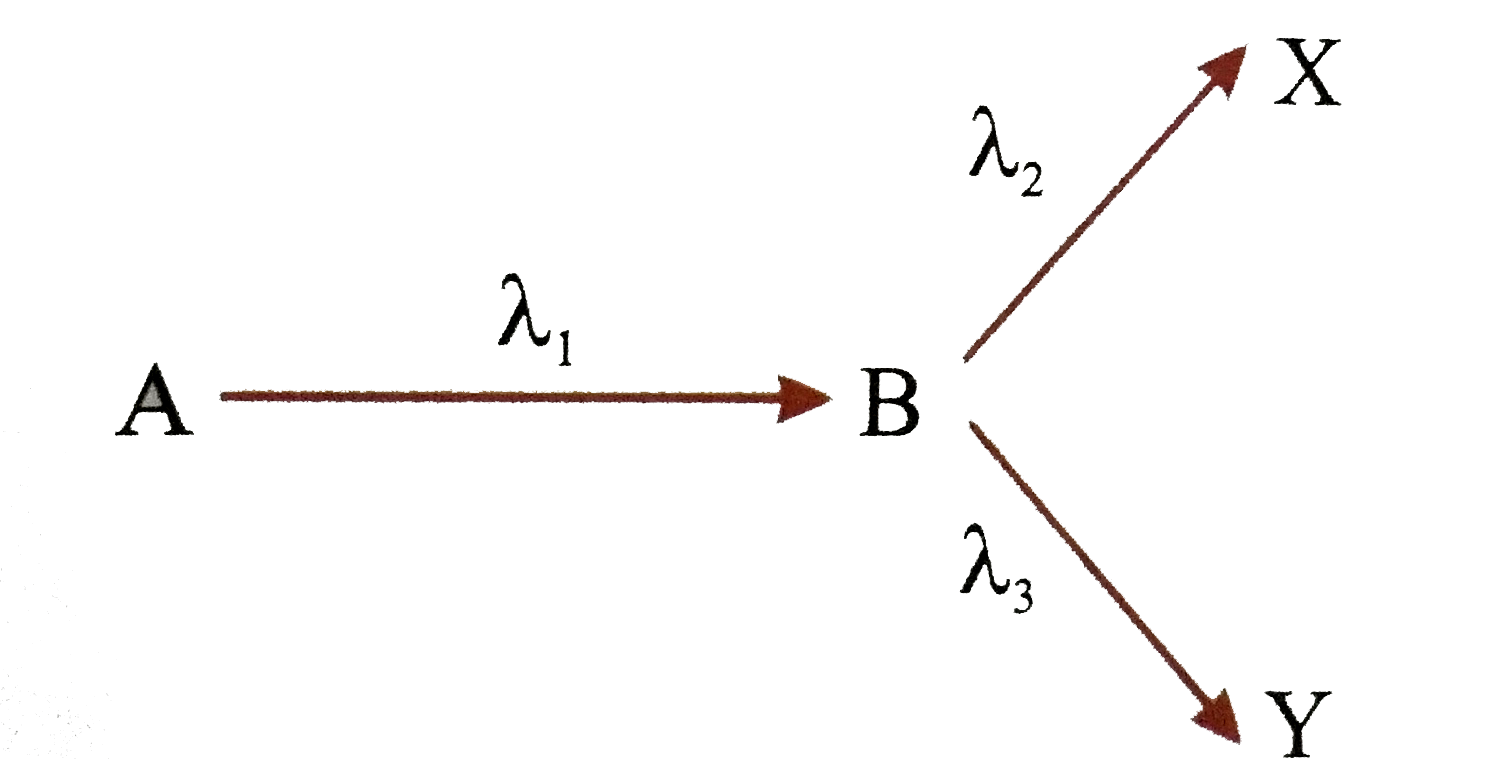
The number of nuclei of B will first increase and then after a maximum value, it decreases forAλ1>λ2+λ3Bλ1=λ2=λ3Cλ1=λ2+λ3DFor any values of λ1,λ2 and λ3 - Question 3 - Select One
The rate at which a particular decay process occurs in a radio active sample, is proportional to the number of radio active nuclei present. If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN.
_E01_161_Q01.png)
Consider radioavtive decay of A to B which may further decay, either to X or to Y, λ1,λ2 and λ3 are decay constants for A to B decay, B to X decay and B of Y decay respectively. If at t=0 number of nuclei of A, B, X and Y are N0,N0, zero and zero respectively and N1,N2,N3,N4 are number of nuclei A,B,X and Y at any intant.
At t=∞, which of the following is incorrect ?AN2=0BN3=N0λ2λ2+λ3CN4=2N0λ3λ2+λ3DN3+N4+N1+N2=2N0
The rate at which a particular decay process occurs in a radio sample, is proportional to the number of radio active nuclei present . If N is the number of radio active nuclei present at some instant, the rate of change of N is dNdt=−λN. Consider radioactive decay of A to B which may further decay either to X or to Y, λ1,λ2andλ3 are decay constants for A to B decay , B to X decay and B of Y decay respectively. if at t=0 number of nuclei of A,B , X and Y are N0,N0,zero and zero respectively
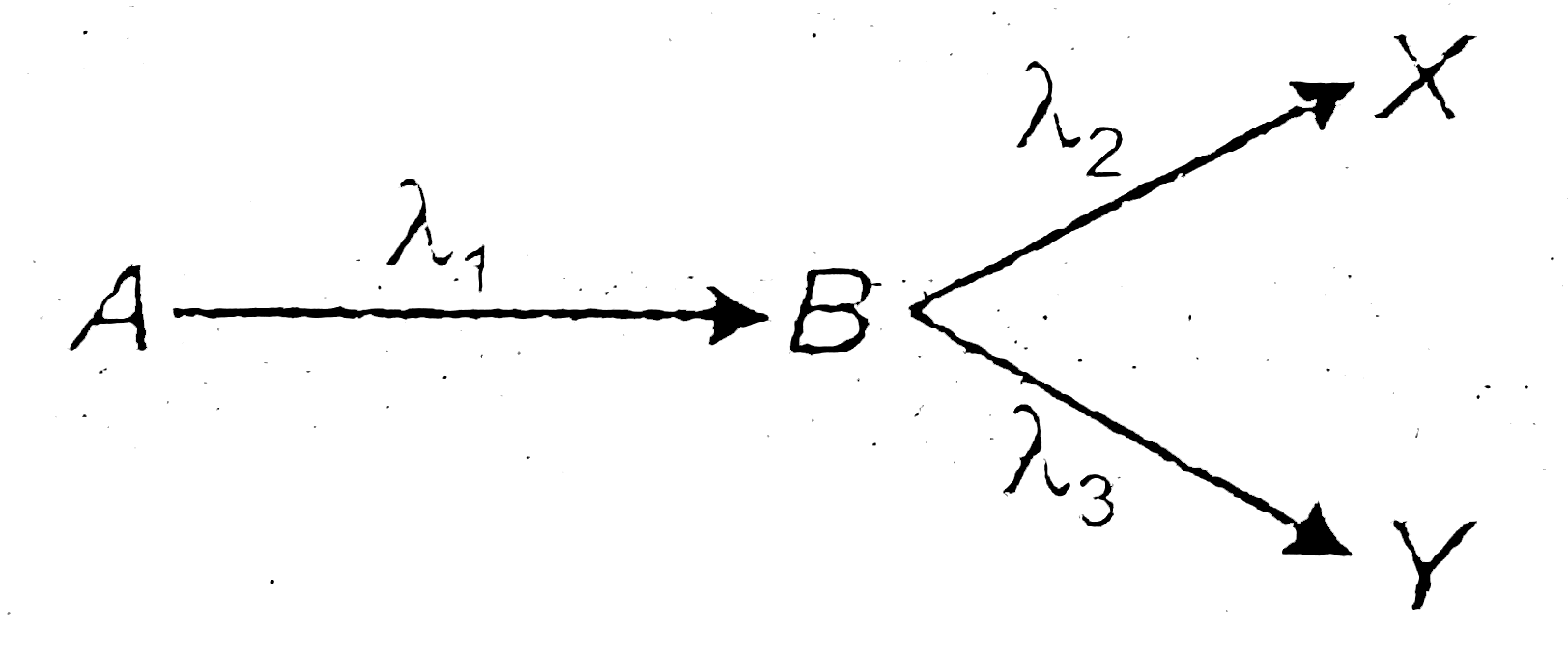
and N1,N2,N3,N4 are number of nuclei A,B , X and Y at any instant.
The number of nuclei of B will first increase then after a maximum value, it will decreases, ifView SolutionTwo radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionA radioactive nuclide can decay simultaneously by two different processes which have decay constants λ1 and λ2. The effective decay constant of the nuclides is λ.
View SolutionA radioactive nuclide can decay simultaneously by two different processes which have decay constant λ1 and λ2. The effective decay constant of the nucleide is λ
View Solution

