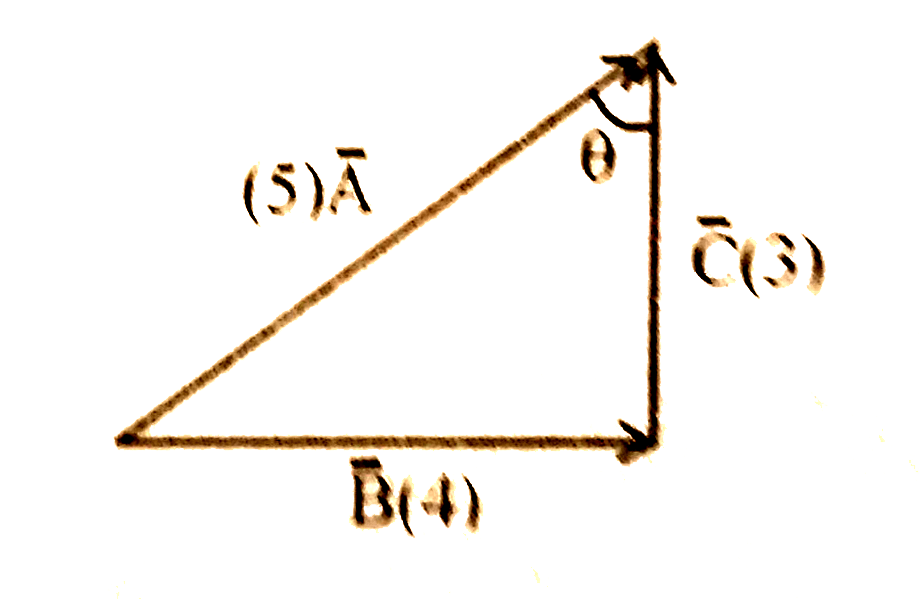
If $\to A = \to B + \to C$ and the magnitude of $\to A, \to B and \to C$ are 5, 4, and 3 units respectively the angle between $\to A and \to B$ is :

A

${cos}^{- 1} (3 / 5)$

B

${cos}^{- 1} (4 / 5)$

C

$π / 2$

D

${sin}^{- 1} (3 / 4)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$tan . θ = \frac{4}{3}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32videos
TEST PAPERS
BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3videos
TEST PAPERS
BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4videos
TEST PAPERS
BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32videos
SEMICONDUCTORS

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to A = \to B + \to C$ , and the magnitudes of $\to A$ , $\to B$ , $\to C$ are 5,4, and 3 units, then the angle between $\to A$ and $\to C$ is
A ${cos}^{- 1} (\frac{3}{5})$
B ${cos}^{- 1} (\frac{4}{5})$
C ${sin}^{- 1} (\frac{3}{4})$
D $\frac{π}{2}$
Question 2 - Select One
The magnitudes of vectors $\to A, \to B and \to C$ are 3,4 and 5 unit respectively. If $\to A + \to B = \to C,$ the angle between $\to A and \to B$ is
A $\frac{π}{2}$
B ${cos}^{- 1} (0.6)$
C ${tan}^{- 1} (\frac{7}{5})$
D $\frac{π}{4}$
Question 3 - Select One
The magnitude of vectors $\to A, \to B and \to C$ are 3, 4 and 5 units respectively. If $\to A + \to B = \to C$ , the angle between $\to A and \to B$ is
A $\frac{π}{2}$
B $\frac{π}{4}$
C ${tan}^{- 1} (\frac{7}{5})$
D ${cos}^{- 1} (0.6)$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile