In the shown figure.

Column IColumn II(A)if μ1=0,μ=0, then for block m(P)Work dine by normal force between the wedge and block is always positive in ground frame.(B)ifμ1=0,μ2=0, then for wedge M.(Q)Work done by normal force between the wedge and block is always negative or zero in ground frame.(C)if μ1≠0,μ1=0, then for block m.(R)Work done by constact force between the wedge and block is always negative in ground frame.(S)Work done by friction force betwen the wedge and ground is always negative in ground frame.
The correct Answer is:(A) = QR, (B) = P, (C ) = Q
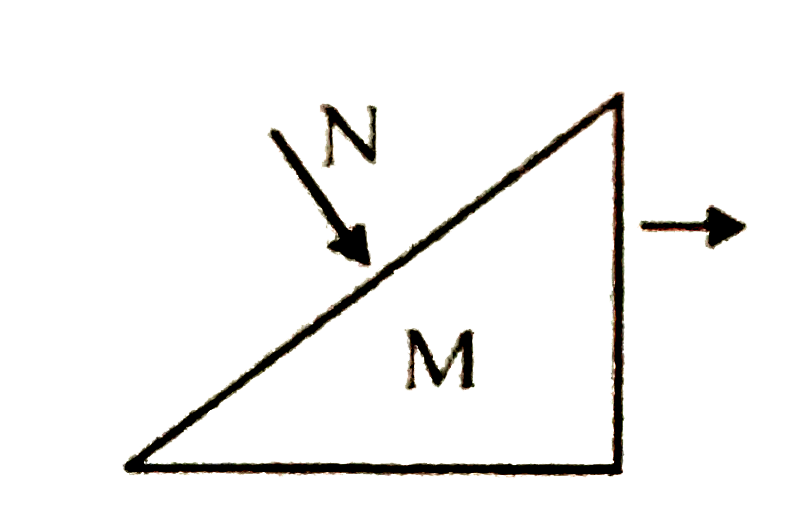
(A) Wedge slides towards right. So work of N is +ve on wedge.
As total work of N on system is 0, so WN on block is −ve.
(C ) Case (1) wedge does not slide on ground WN=0
Case (2) Wedge slides on ground towards right.
So WN on wedge is +ve
Then WN on block has to be −ve
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART A
12 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART B
1 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART A
35 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Two small blcok m=2kg each kept on wedge of mass 12kg. There is no friction between blocks and wedge coefficient of friction between wedge and ground in μ=0.3. Calculate frictional force by ground on wedge.
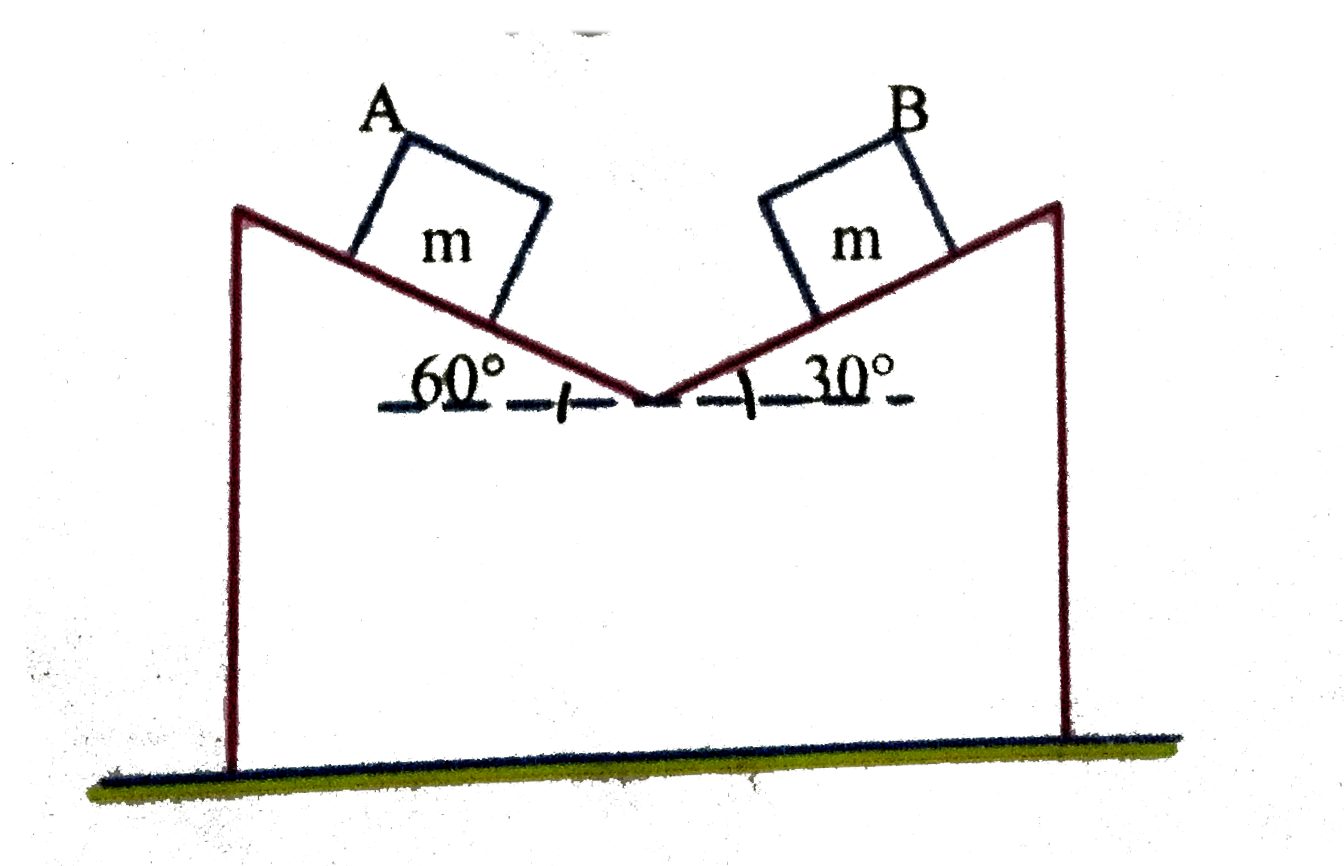
View SolutionThe coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View Solution
Knowledge Check
In which of the following cases the friction force between 'A' and 'B' is maximum. In all cases μ1=0.5,μ2=0.
A B
B C
C D
D
A block is released on the slant face of a wedge of equal mass placed on a horizontal floor. The slant face of the wedge makes an angle of 45∘ with the floor. Coefficient of friction between all surfaces in contact is the same. Different value/ range of coefficient of friction is given in column I and corresponding consequences in column II and III (wedge is fress to move)

Column-IColumn-IIColumn-III(I)μ=0(i)Work done by friction on block and wedge is negative (on each)(P)Centre of mass of system (block+wedge) moves rightward and downward(II)μ>1(ii)Work done by friction on block is negative but on wedge it is zero(Q)Centre of mass of system (block+wedge) moves leftward and downward(III)√5−2<μ<1(iii)Work done by friction on block and wedge is zero (on each)(R)Centre of mass of system (block+wedge) remains at rest(IV)μ<√5−2(iv)Friction between the block and wedge is static and between the wedge and ground it is kinetic in nature.(S)Centre of mass of system (block+wedge) moves vertically downward
Which of the following options is the correct representaion of the case that the block slides down the wedge and wedge slide on the floorA(I)(iv)PB(III)(iii)QC(IV)(i)QD(II)(iii)(R)
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionThe coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.
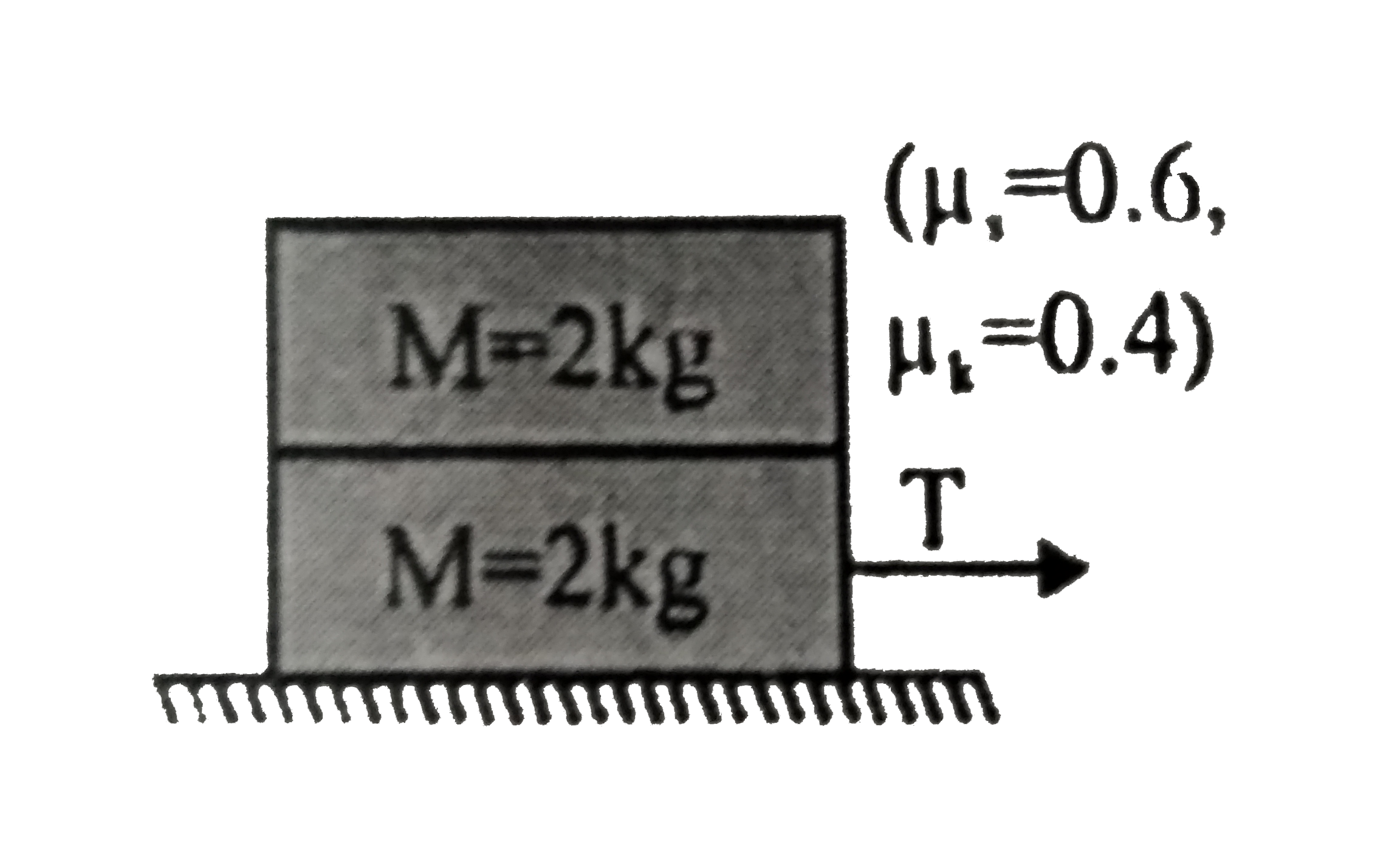
View SolutionThe coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.

View SolutionIn which of the following cases the friction force between 'A' and 'B' is maximum. In all cases μ1=0.5,μ2=0.
View SolutionFind the ratio of work done by gravity on the block under the two conditions. Assume μ=0 between block and plane.

View SolutionFind the ratio of work done by gravity on the block under the two conditions. Assume μ=0 between block and plane.

View Solution
