The coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
The correct Answer is:Q=mMgcosαcosφMcosφ+msinαsin(α−φ)
The equation of motion will assume the form (see fig.)
−Qsinα+Tcosα=Mbx
Qsinα−Tcosα=max, −mg+Qcosα+Tsinα=may
ay=(−ax+bx)tanα,T=μQ
Hence Q=mMgcosαM+msinα(sinα−μcosα)
ax=Mgcosα(sinα−μcosα)M+msinα(sinα−μcosα)
bx=−mgcosα(sinα−μcosα)M+msinα(sinα−μcosα)
ay=−(M+m)gsinα(sinα−μcosα)M+msinα(sinα−μcosα)
The block can either slide down the wedge, or remain stationary. It can slide down if sinα>μcosα, i.e. if tanα>μ. In this case
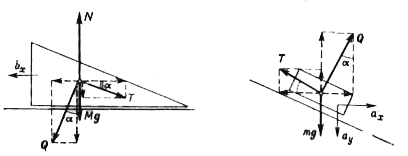
ax>0,ay<0andbx<0. If, on the other hand, tanα≤μ, the block and the wedge will remain stationary.
Similar Questions
Knowledge Check
a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
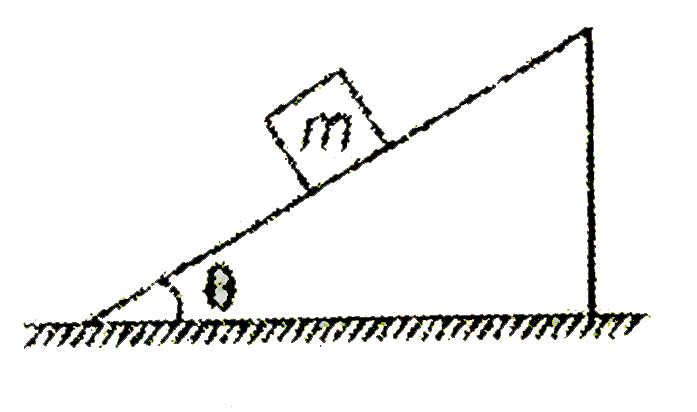 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
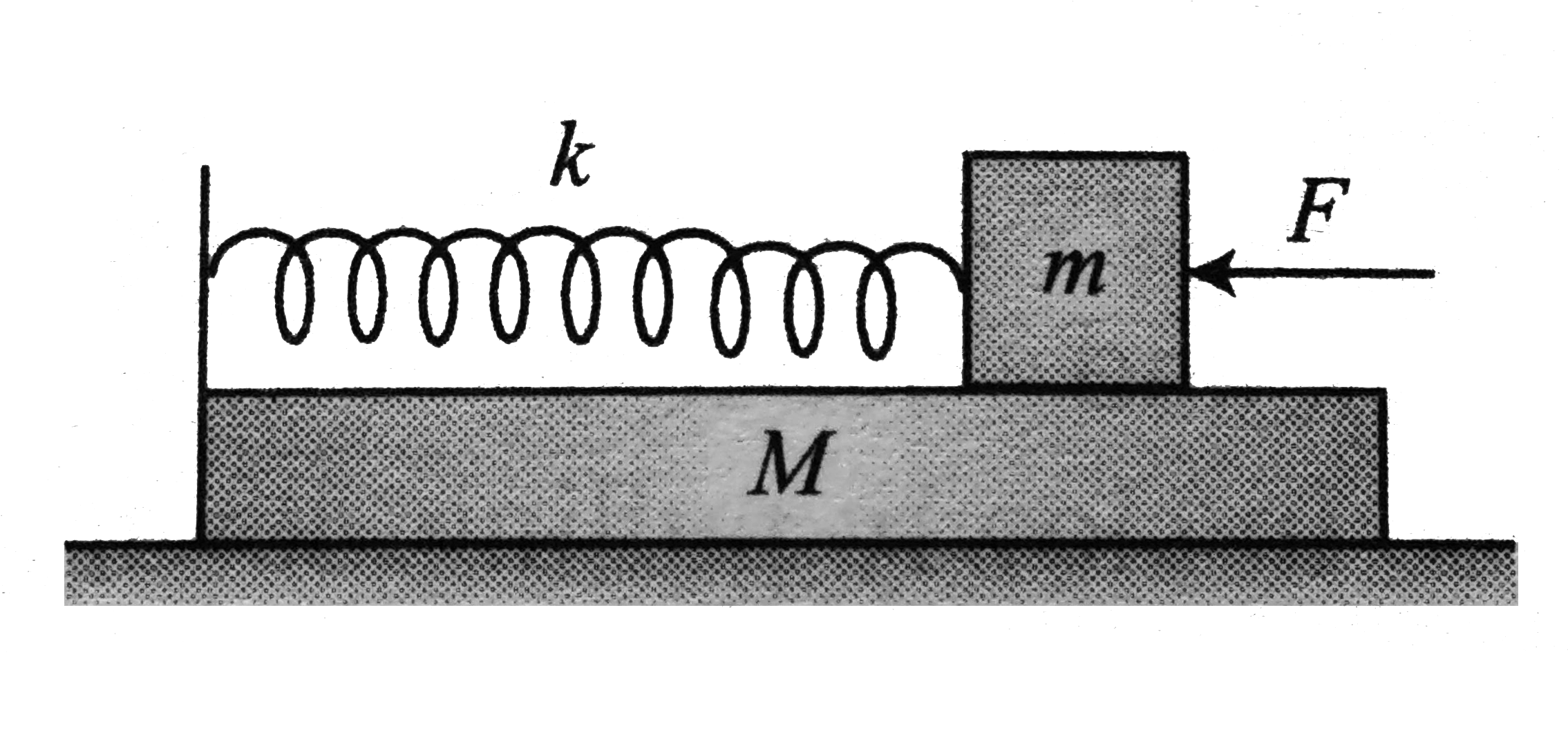
View SolutionA constant force F pushes the block m till the wedge M starts sliding. If the stiffness of the light spring connecting M and m is K, coefficient of friction between block and wedge is μ1 and between the wedge and ground is μ2, find the value of the force F
View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,

View SolutionA constant force F pushes the block m till the wedge M starts sliding. If the stiffness of the light spring connecting M and m is K, coefficient of friction between block and wedge is μ1 and between the wedge and ground is μ2, find the minimum value of the force F

View SolutionThe block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3
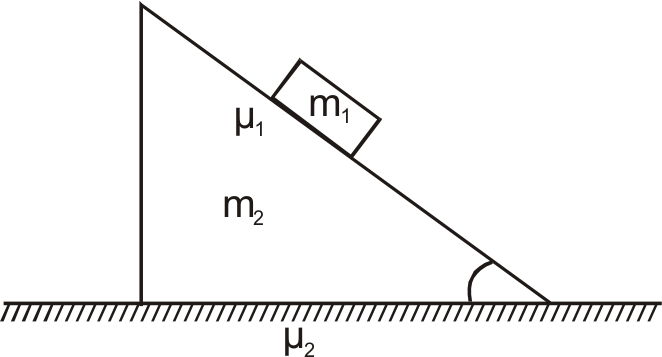
View SolutionThe block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3

View SolutionThe block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3

View Solution
