A unifrom semicircular disc is suspended from a point C on it such that it remains in vertical plane. It is found that point C is such that disc remains in equilibrium in every orientation. What is distance OC ?

1 m
1.5 m
1.33 m
1.83 m
The correct Answer is:C
To remain in equilibrium C must be CM of semicircular disc.
(∴IMg=0)
So OC=4R3π=1.33m
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionFind the distance of instantaneous point of rest, of the disc, from point B.
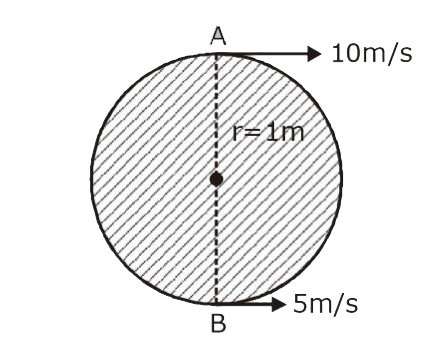
View Solution
Knowledge Check
A thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mA disc is hinged such that it can freely rotate in a vertical plane about a point on its radius. If radius of disc is 'R' , then what will be minimum time period of its simple harmonic motion ?
A2π√RgB2π√3R2gC2π√√2RgD2π√R2gTwo light vertical springs with equal natural length and spring constants k1 and k2 are separated by a distancel. Their upper end the ends A and B of a light horizontal rod AB. A vertical downwards force F is applied at point C on the rod. AB will remain horizontal in equilibrium if the distance AC is
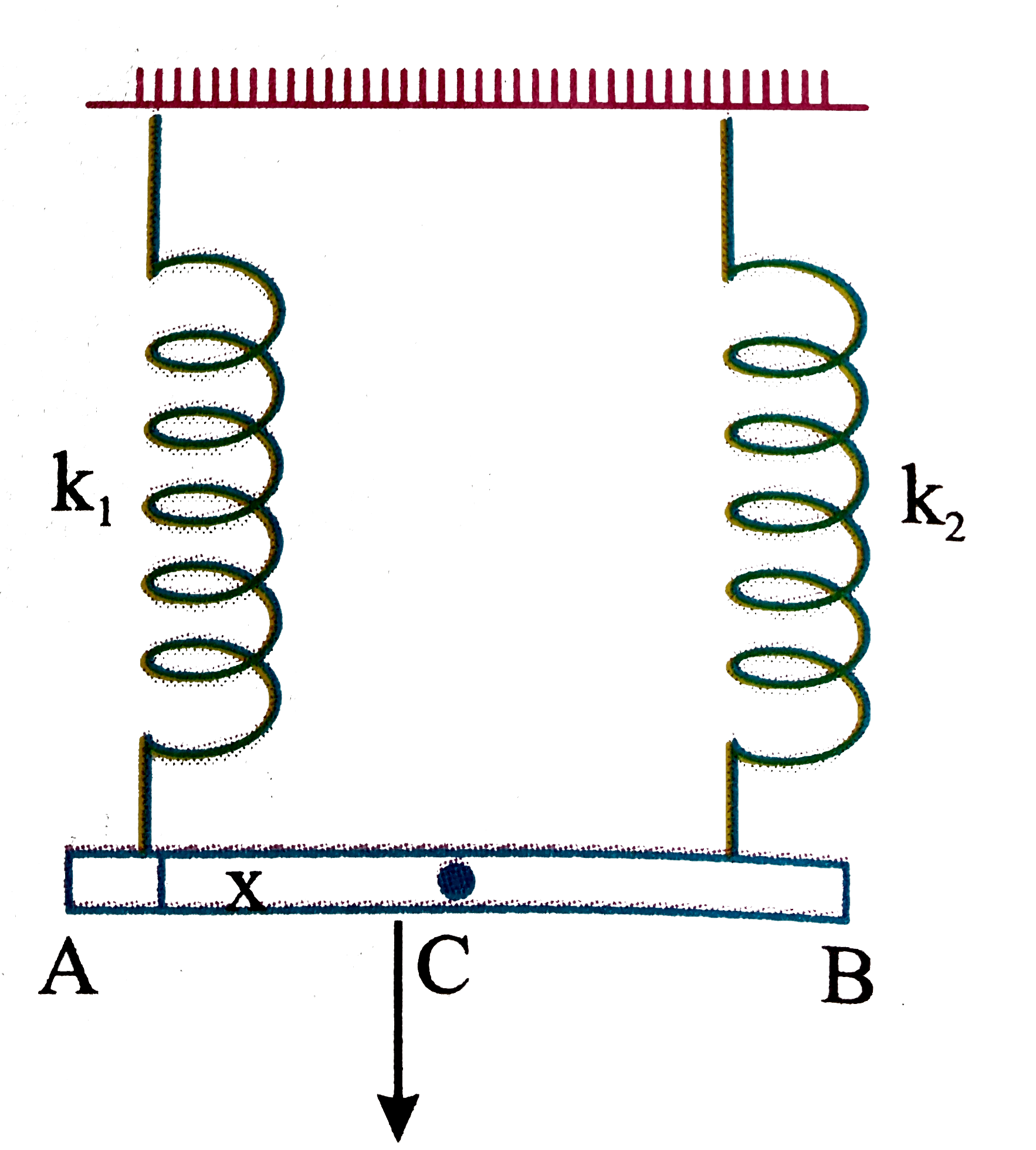 Al2Blk1k1+k2Clk2k1Dlk1k1+k2
Al2Blk1k1+k2Clk2k1Dlk1k1+k2
A uniform circular disc has radius R and mass m. A particle also of mass m is fixed at a point A on the wedge of the disc as in fig. The disc can rotate freely about a fixed horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall so that it tarts rotating about PQ. Find the linear speed of the particle at it reaches its lowest position.
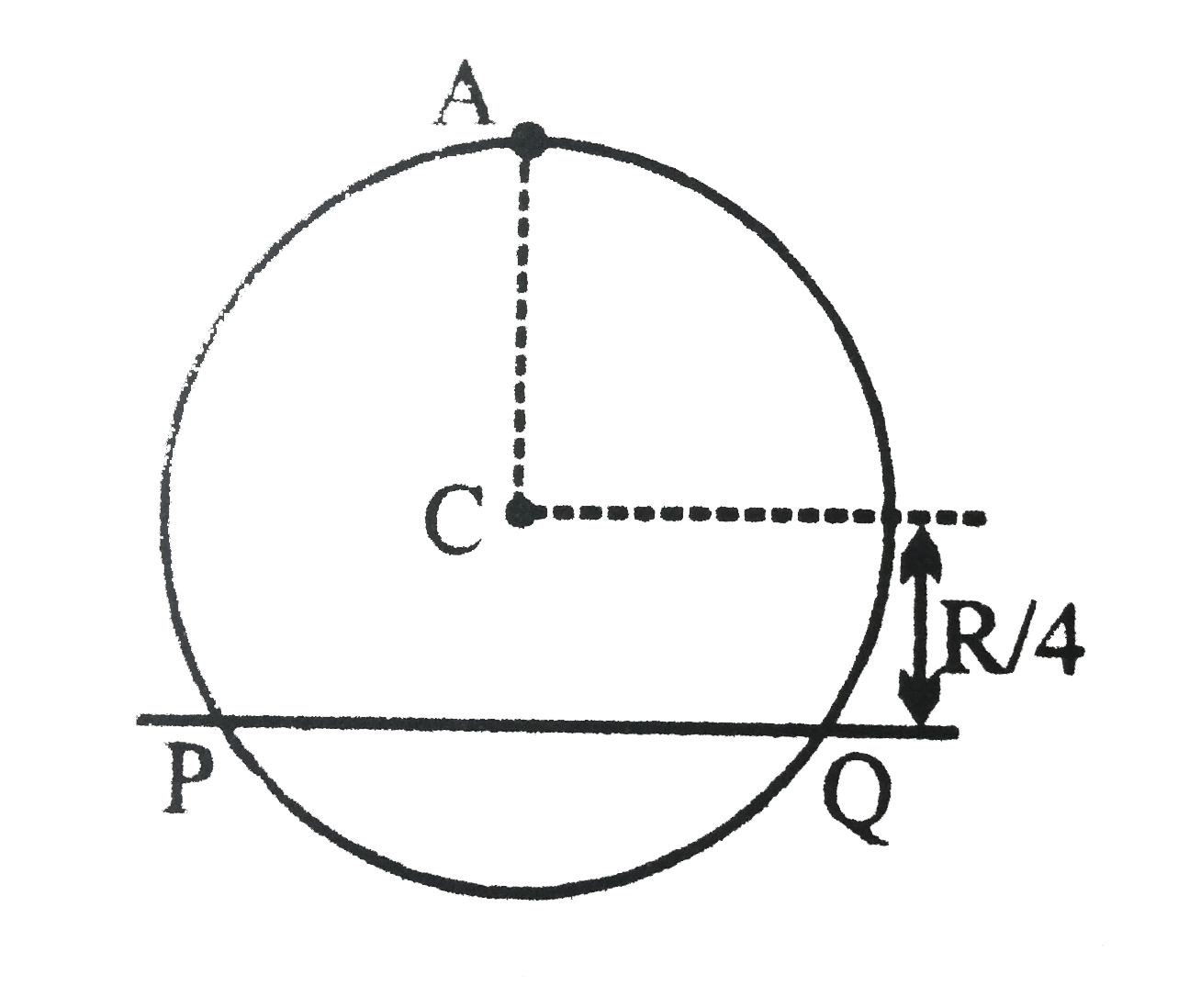 .
.
View SolutionA uniform semicircular disc of mass ' M ' and radius ' R " hinged at point O shown in figure is released from rest from a vertical position as shown. If the initial magnitude of angular acceleration of the disc is xg3πR, then the valuc of x is (Center of mass is at a distance 4R3π from center of disc)
'(##CEN_KSR_PHY_JEE_C09_E01_024_Q13##)'
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
View Solution
