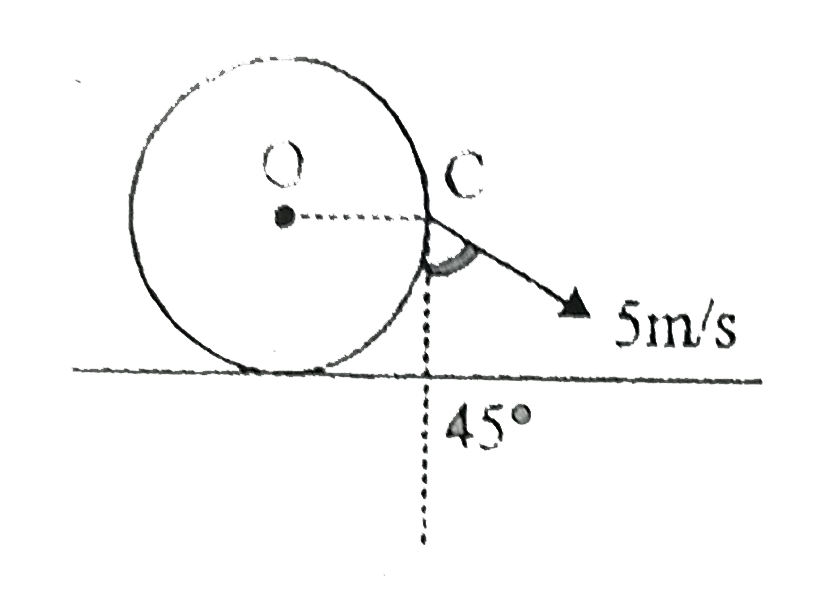
Δ some in tan , a disk of radius 1.0 m is performing rolling on a rough horizontal surface. The velocity of point C in this shown direction is 5m/sec :
Instantaneous centre is at a distance 1.0 m below centre O
Instantaneous centre is at a distance 0.05m below centre O
Angular velocity of disc is (5/√2) rad/sec
Velocity of centre of mass is (5/√2) m/s
The correct Answer is:A, C, D
R=1.0m, M=1.0kg
Velocity of COM = V
Angular velocity of disc =ω
1 is the instantaneous centre.
tan45∘=O1R
OI=Rtan45∘
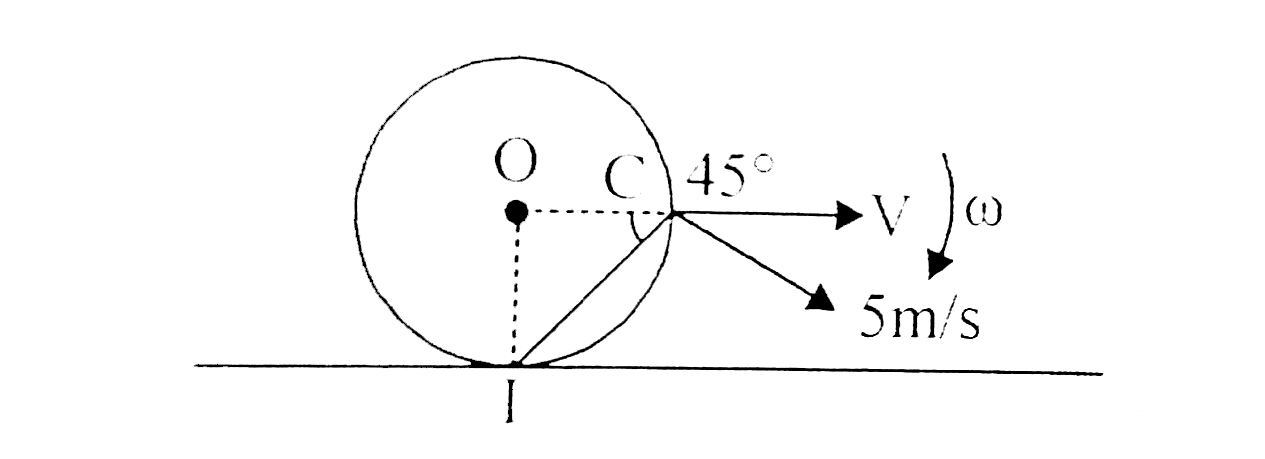
=R=1.0
IC=R√2=√2
ω=VCIC=5√2 rad/sec
V=(OI)ω=(1.0)(5√2)=5√2(m/sec)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART B
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART A
12 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (C )
15 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
An object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be

View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View Solution
Knowledge Check
A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
 A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information
A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient informationA disc of radius R rolls on a rough horizontal surface. The distance covered by the point A in one revolution is
 A2πRB2RC8RDπR
A2πRB2RC8RDπRA ring performs pure rolling on a horizontal surface and its state at some instant of time is shown in figure.
 AK.E. stored in the portion AB is same as K.E. stored in the portion CDBK.E. stored in the portion AB is same as KE. stored in the portion BCCK.E. stored in the portion ABC is same as K.E. stored in the portion CDADK.E. stored in the portion ABC is less than K.E. stored in the portion CDA
AK.E. stored in the portion AB is same as K.E. stored in the portion CDBK.E. stored in the portion AB is same as KE. stored in the portion BCCK.E. stored in the portion ABC is same as K.E. stored in the portion CDADK.E. stored in the portion ABC is less than K.E. stored in the portion CDA
A disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
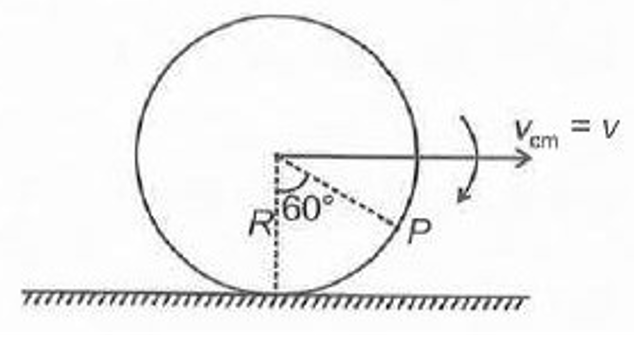
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is

View SolutionAn object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be

View SolutionA solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smooth horizontal surface with a uniform velocity of 0.1 m/s. Its total energy is
View Solution
