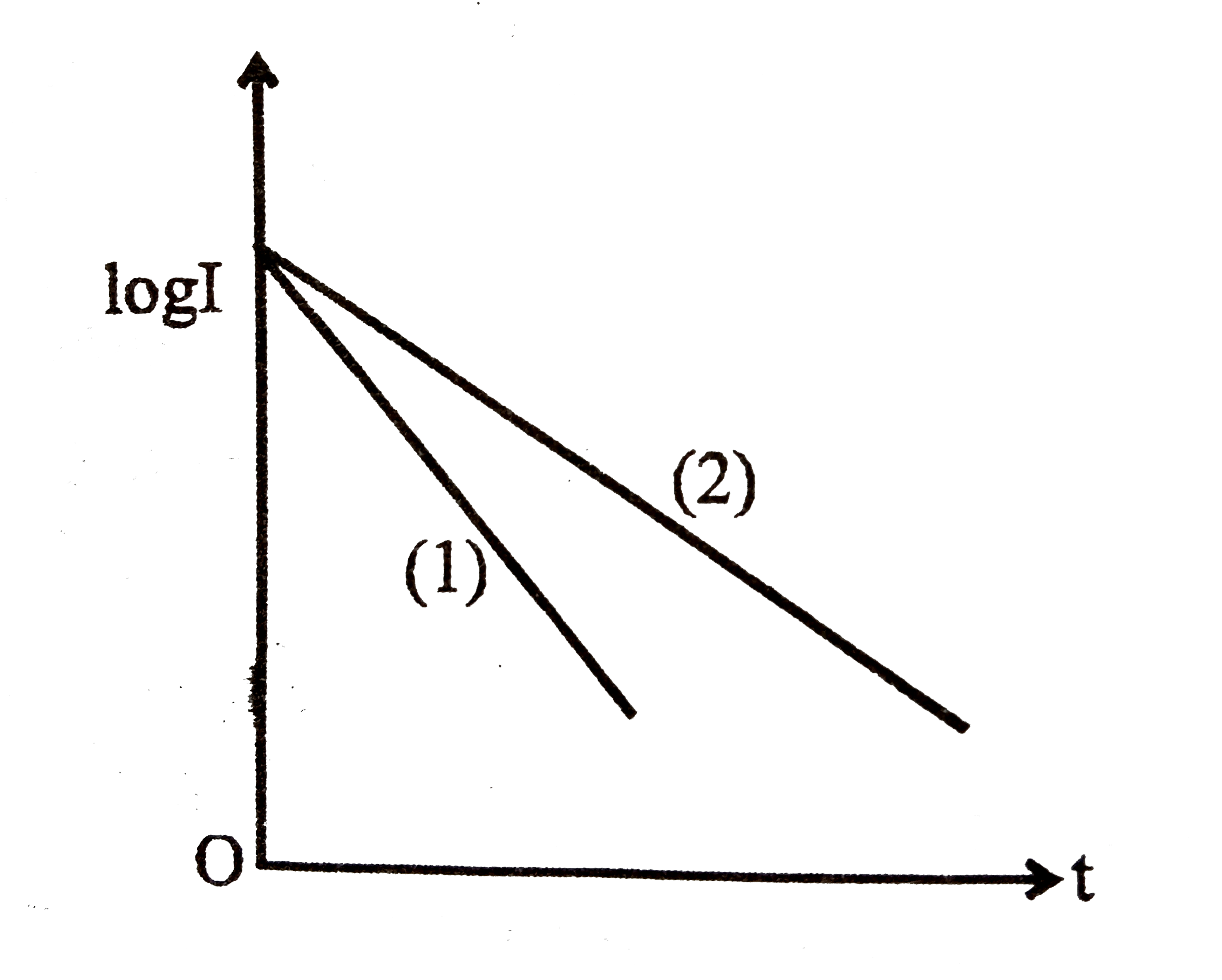
A capacitor of capacitance C is charged to a constant potential difference V and then connected in series with an open key and a pure resistor r. At tiem t=0 , the key is closed. If I is current at time t=0, a plot of log I against t is shown as in the graph (I) . Latter on of the parameters, i.e. V,R and C is changed, keeping the other two constant and graph (2) is recoded. Then -

C is reduced
C is increased
R is reduced
R is increased
The correct Answer is:B
It is discharging of capactior
I=ERe−t/RC
log I=logER−tRC
Intercept is constant ⇒ E & R constant
|slope| dercrease ⇒C↑
Topper's Solved these Questions
Similar Questions
A capacitor of capacity C is charged to a steady potential difference V and connected in series with an opne key and a pure resistor 'R'. At time t=0, the key si closed. If I= current at time t, a plot of logI against 't' is as shown in (1) in the graph. Later one of the parametrs i.e. V,R or C is charged keeping the other two constant, and graph (2) is recored. then-
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View Solution
Knowledge Check
A capacitor of capacity C is charged to a steady potential difference V and connected in series with an opne key and a pure resistor 'R'. At time t=0, the key si closed. If I= current at time t, a plot of logI against 't' is as shown in (1) in the graph. Later one of the parametrs i.e. V,R or C is charged keeping the other two constant, and graph (2) is recored. then-
 AC is reducedBC is increasedCR is reducedDR is increased
AC is reducedBC is increasedCR is reducedDR is increasedA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)VTwo identical capacitors eachof capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charges on the capacitor at t=CR are
 ACVe,CVeBCV, CVCVCe,VCDVC,VCe
ACVe,CVeBCV, CVCVCe,VCDVC,VCe
A capacitor of capacitance C is charged to a voltage V0 and subsequently discharged through a combination of a resistor R and another identical capacitor C in series. Find the current at time t and heat generated in the same time.
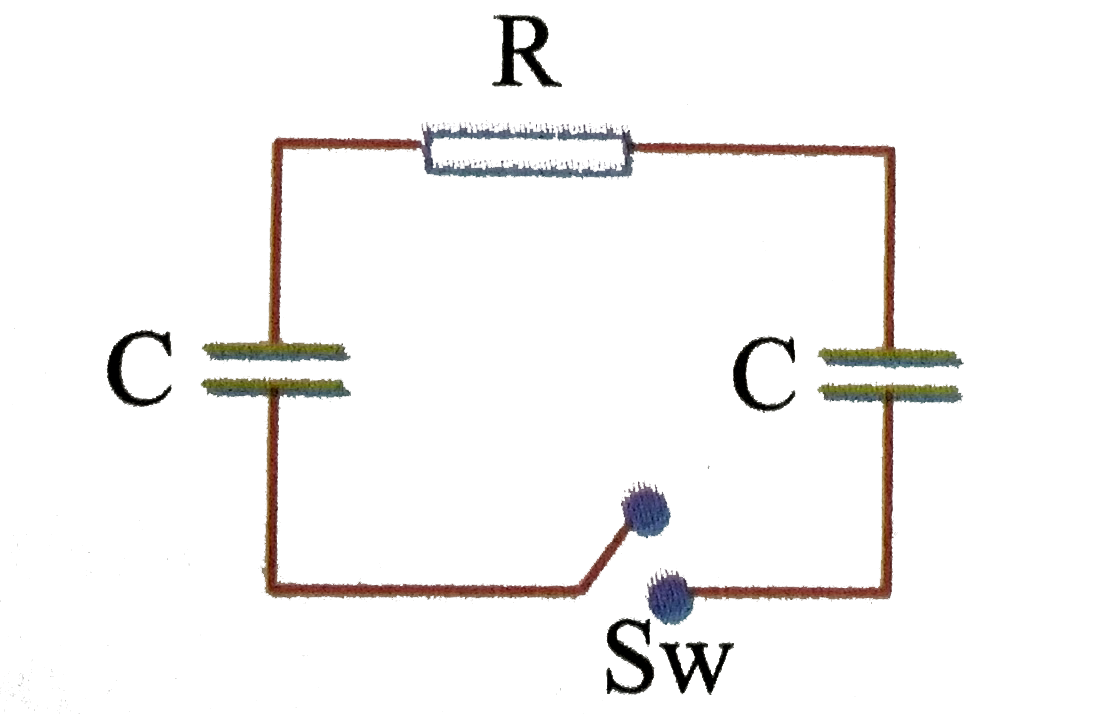
View SolutionIn the circuit shown, a capacitor charged to a potential difference V0 is connected to an uncharged capacitor through a resistor at t=0, by closing the switch. Find current in the circuit as function of time.
 .
.
View SolutionA capacitor of capacitance C is connected to a battery of emf V through a resistance R with a switch connected in series .Switch is turned on at t=0 . Find the displacement current flowing between the plates of capacitor as a function of time .
View SolutionTwo identical capacitors each of capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charged on the capacitor at t=CR are
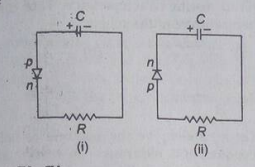
View SolutionTwo identical capacitors each of capacitance C are charged to the same potential V and are connected in two circuits (i) and (ii) at t=0 as shown. The charged on the capacitor at t=CR are

View Solution
