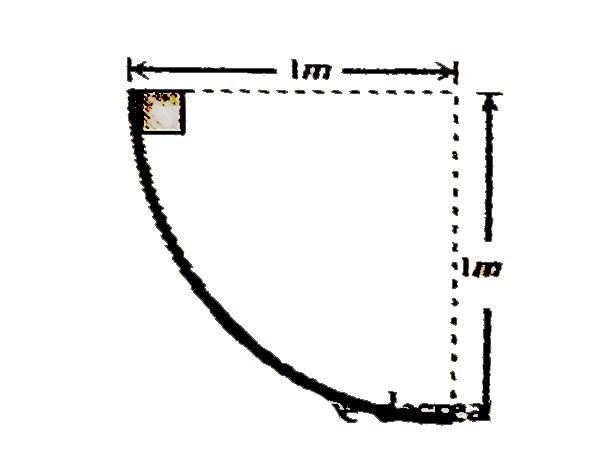
A body of mass 2kg slides down a curved track which is quadrant of a circle of radius 1 metre . All the surfaces are frictionless. If the body starts from rest, its speed at the bottom of the track is

A

$4.43 m s^{- 1}$

B

$2 m s^{- 1}$

C

$0.5 m s^{- 1}$

D

$19.6 m s^{- 1}$

Video Solution

Text Solution

Verified by Experts

Equating gain of kinetic energy with loss of gravitational potential energy, we get
$\frac{1}{2} m v^{2} = m g h$
or $v = \sqrt{2} g h$
or $v = \sqrt{2 \times .9 .8 \times 1} m s^{- 1} < b r >$ v=sqrt(19.6)" "ms^(-1)=4.43ms^(-1)

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A body slides down a fixed curved track that is one quadrant of a circle of radius $R$ , as in the figure. If there is no friction and the body starts from rest, its speed at the bottom of the track is
A $5 g R$
B $\sqrt{5 g R}$
C $\sqrt{2 g R}$
D $\sqrt{g R}$
Question 2 - Select One
A block of mass 1 kg slides down a vertical curved track that is one quadrant of a circle of radius 1m. Its speed ast the the bottom si $2 m / s$ . The work done by frictional force is :

A $8 J$
B $- 8 J$
C $4 J$
D $- 4 J$
Question 3 - Select One
A block of mass $1 k g$ slides down a curved track which forms one quadrant of a circle of radius $1 m$ as shown in figure. The speed of block at the bottom of track is $v = 2 m s^{- 1}$ . The work done by the of friction is
.
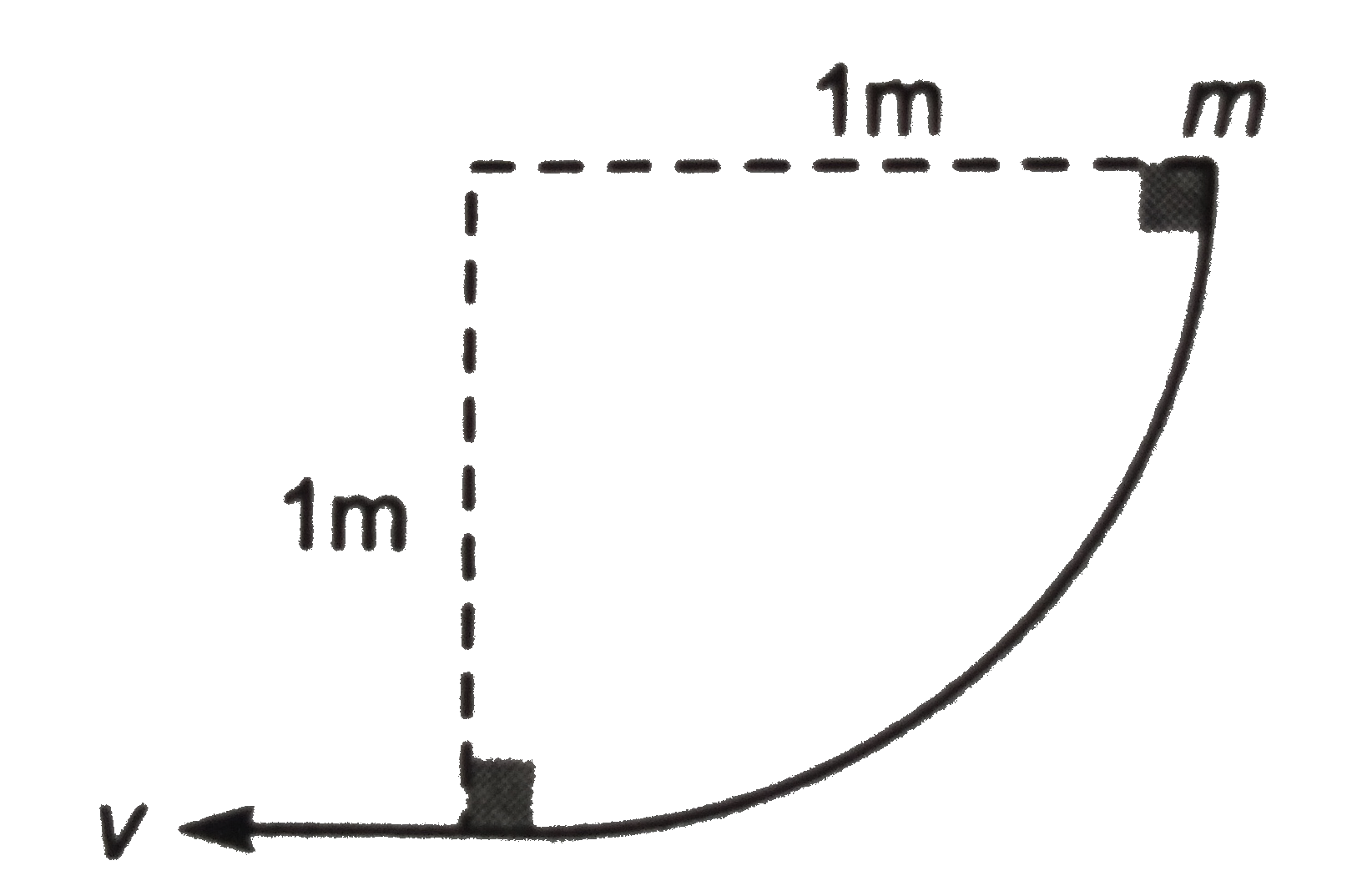A $+ 4 J$
B $- 4 J$
C $- 8 J$
D $+ 8 J$

CAREER POINT-REVISION TEST 1-PHYSICS

Home
Ask Doubt
Profile