It is tempting to think that all possible transitions are permissible,

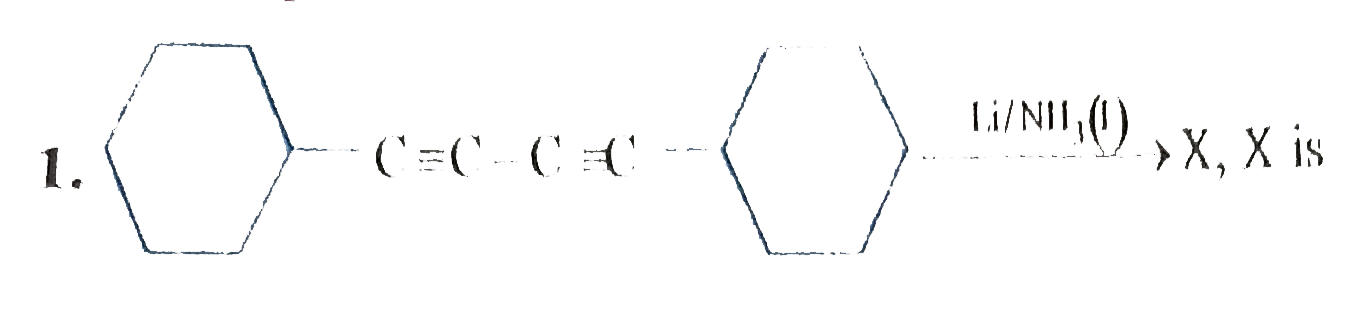Complete the following reaction ocr_image

ocr_image
Identify the position where electrophilic aromatic substitution EAS) is most favourable

It is teming to think that all possible transituion are permissible and that an atomic spectrum series from the transition of an electron from any intial orbital to any other .However this is not so because a photon a photon has as intrinsic spin angular momentum of $\sqrt{2} h / 2 π$ corresponding to $S = 1$ although it has no charge and no rest mass
On the other hand , an electron has got two typwe of agular momentum orbit angular momentum
$L = [\sqrt{l (l + 1)}] h / 2 π$ ,and spin angular momentum $L_{1} = \sqrt{s (s + 1)} h / 2 π$ arising from orbital motion and spin motion of the electronn during any electton transition must compentum for the angular momentum carried away by the photon .To salary this condition the different between the azisition quantum number of teh orbital witjhin which the transition $(l = 2)$ cannot make a transition into as x-orbital $(l = 0)$ because the photon cannot carry away enough angular momentum
Electron transition from $4 s$ to $3 s$ orbital is forbiddeon meating that it cannot because

01:33

View Solution

It is teming to think that all possible transituion are permissible and that an atomic spectrum series from the transition of an electron from any intial orbital to any other .However this is not so because a photon a photon has as intrinsic spin angular momentum of $\sqrt{2} h / 2 π$ corresponding to $S = 1$ although it has no charge and no rest mass
On the other hand , an electron has got two typwe of agular momentum orbit angular momentum
$L = [\sqrt{l (l + 1)}] h / 2 π$ ,and spin angular momentum $L_{1} = \sqrt{s (s + 1)} h / 2 π$ arising from orbital motion and spin motion of the electronn during any electton transition must compentum for the angular momentum carried away by the photon .To salary this condition the different between the azisition quantum number of teh orbital witjhin which the transition $(l = 2)$ cannot make a transition into as x-orbital $(l = 0)$ because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electon with $n = 5$ is

01:16

View Solution

Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum Spin angular momentum =sqrt(s(s+1))h Orbital angular momentum =sqrt(l(l+1))h Total spin of ana tom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity =(2sums+1) Q. The orbital angular momentum of a 2p-electron is:

02:54

View Solution

It is tempting to think that all possible transitions are permissible, and that an atomic spectrum arises from the transition of an electron from nay initial orbital to any other orbital. However, this is no so, because a photon has an intrinsic spin angular momentum of sqrt(2)(h)/(2pi) corresponding to S = 1 although it has no charge and no rest mass. on the otherhand, an electron has got two types of angular momentum: Orbital angular momentum, L = = sqrt(l(l+1))(h)/(2pi) and spin angular momentum, L_(s) (=sqrt(s(s+1))(h)/(2pi)) arising from orbital motion and spin motion of electron respectively. The change in angular momentum of the electron during any electronic transition must compensate for the angular momentum carried away by the photon. To satisfy this condition the difference between the azimuthal quantum numbers of the orbitals within which transition takes place must differ by one. Thus, an electron in a d-orbital (l=2) cannot make a transition into an s-orbital (l=0) because the photon cannot carry away enough angular momentum. An electron, possess four quantum numbers, n l, m and s. Out of these four l determines the magnitude of orbital angular momentum (mentioned above) while m determines its Z-component as m((h)/(2pi)) . The permissible values of only integers right from -l to +l . While those for l are also integers starting from 0 to (n-1) . The values of l denotes the sub-shell. For l = 0,1,2,3,4... the sub-shells are denoted by the symbols s,p,d,f,g....respectively. The maximum orbital angular momentum of an electron with n = 4 is

View Solution

It is tempting to think that all possible transitions are permissible, and that an atomic spectrum arises from the transition of an electron from nay initial orbital to any other orbital. However, this is no so, because a photon has an intrinsic spin angular momentum of sqrt(2)(h)/(2pi) corresponding to S = 1 although it has no charge and no rest mass. on the otherhand, an electron has got two types of angular momentum: Orbital angular momentum, L = = sqrt(l(l+1))(h)/(2pi) and spin angular momentum, L_(s) (=sqrt(s(s+1))(h)/(2pi)) arising from orbital motion and spin motion of electron respectively. The change in angular momentum of the electron during any electronic transition must compensate for the angular momentum carried away by the photon. To satisfy this condition the difference between the azimuthal quantum numbers of the orbitals within which transition takes place must differ by one. Thus, an electron in a d-orbital (l=2) cannot make a transition into an s-orbital (l=0) because the photon cannot carry away enough angular momentum. An electron, possess four quantum numbers, n l, m and s. Out of these four l determines the magnitude of orbital angular momentum (mentioned above) while m determines its Z-component as m((h)/(2pi)) . The permissible values of only integers right from -l to +l . While those for l are also integers starting from 0 to (n-1) . The values of l denotes the sub-shell. For l = 0,1,2,3,4... the sub-shells are denoted by the symbols s,p,d,f,g....respectively. The orbital angular momentum of an electron in p-orbital makes an angle of 45^(@) from Z-axis. Hence Z-component of orbital angular momentum of electron is: