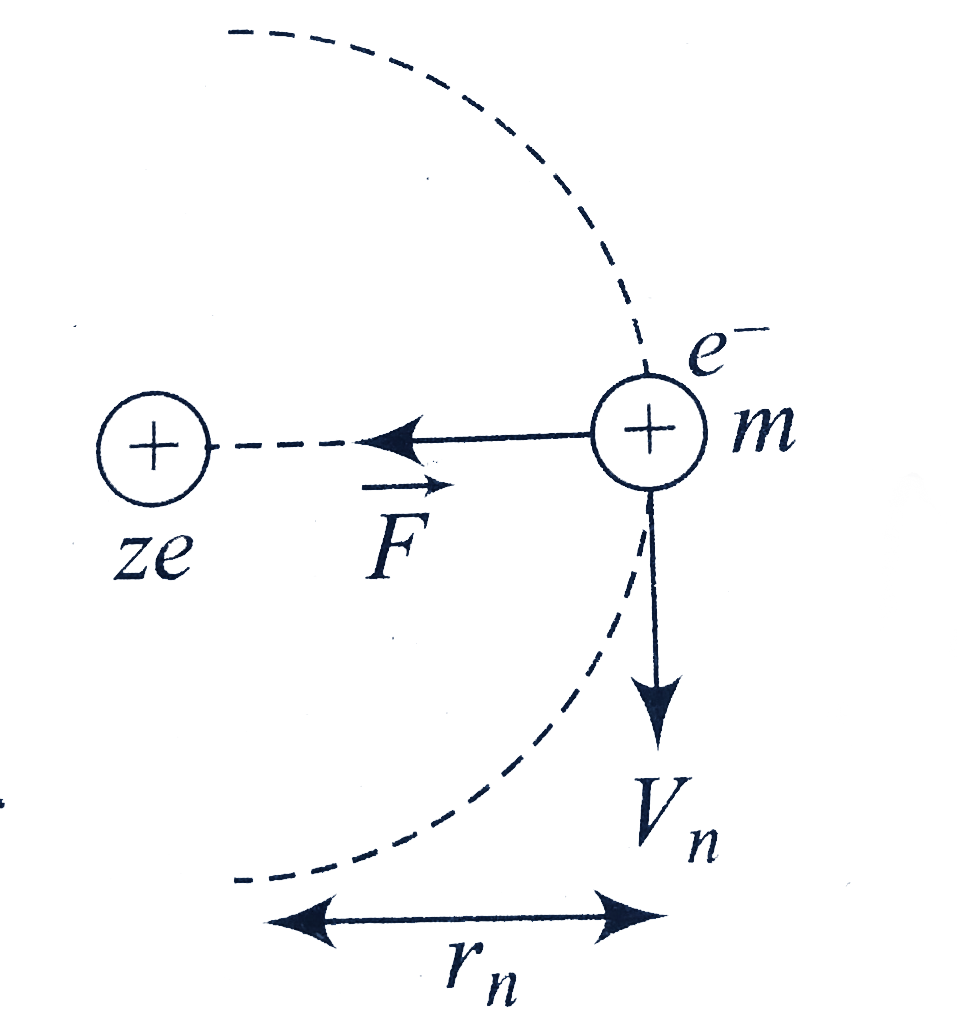
In a hydrogen like ion, nucleus has a positive charge Ze, Bohr's quantization rule is, the angular momentum of an electron about the nucleus l=nh2π, where 'n' is a positive integer.
Change in K.E of electron when it goes from ground state to 1st excited state
332meze4∈20h2
−332meze4∈20h2
132meze2∈20h2
−132meze2∈20h2
The correct Answer is:B
K.E.=− (Total Energy)
ΔKE=−32zme4∈20h2
Topper's Solved these Questions
Similar Questions
A hydrogen atom is in a state with energy −1.51eV. in the Bohr model, what is the angular momentum of the electron in the atom with respect to an axis at the nucleus?
View SolutionA hydrogen atom is in its excited state with energy -1.51 eV. The angular momentum of the electron in this state is xh2π then write the value of 'x'
View Solution
Knowledge Check
- Question 1 - Select One
In a hydrogen like ion, nucleus has a positive charge Ze, Bohr's quantization rule is, the angular momentum of an electron about the nucleus l=nh2π, where 'n' is a positive integer.
If electron goes from ground state to 1st excited state then change in energy of the hydrogen like ion isA332mez2e4∈20h2B132meze4∈20h2C332meze2∈20h2D132meze2∈20h2 - Question 2 - Select One
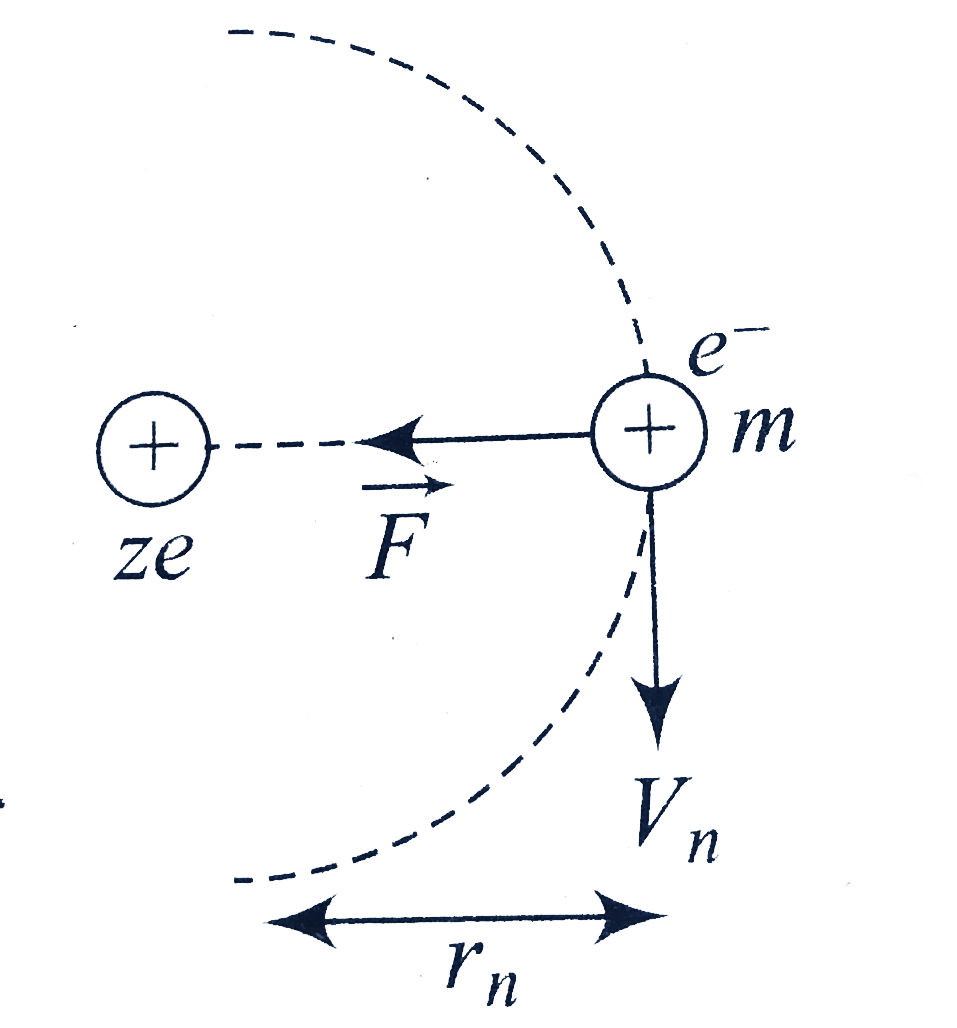
In a hydrogen like ion, nucleus has a positive charge Ze, Bohr's quantization rule is, the angular momentum of an electron about the nucleus l=nh2π, where 'n' is a positive integer.
If electron is in ground state the magnetic field produced at the site of nucleus due to circular motion of the electronAμ0Z38πe7m2∈30h5Bμ0Z28πe7m2∈30h5Cμ0πZ38e7m2∈30h5Dμ0πZ28e7m2∈30h5 - Question 3 - Select One
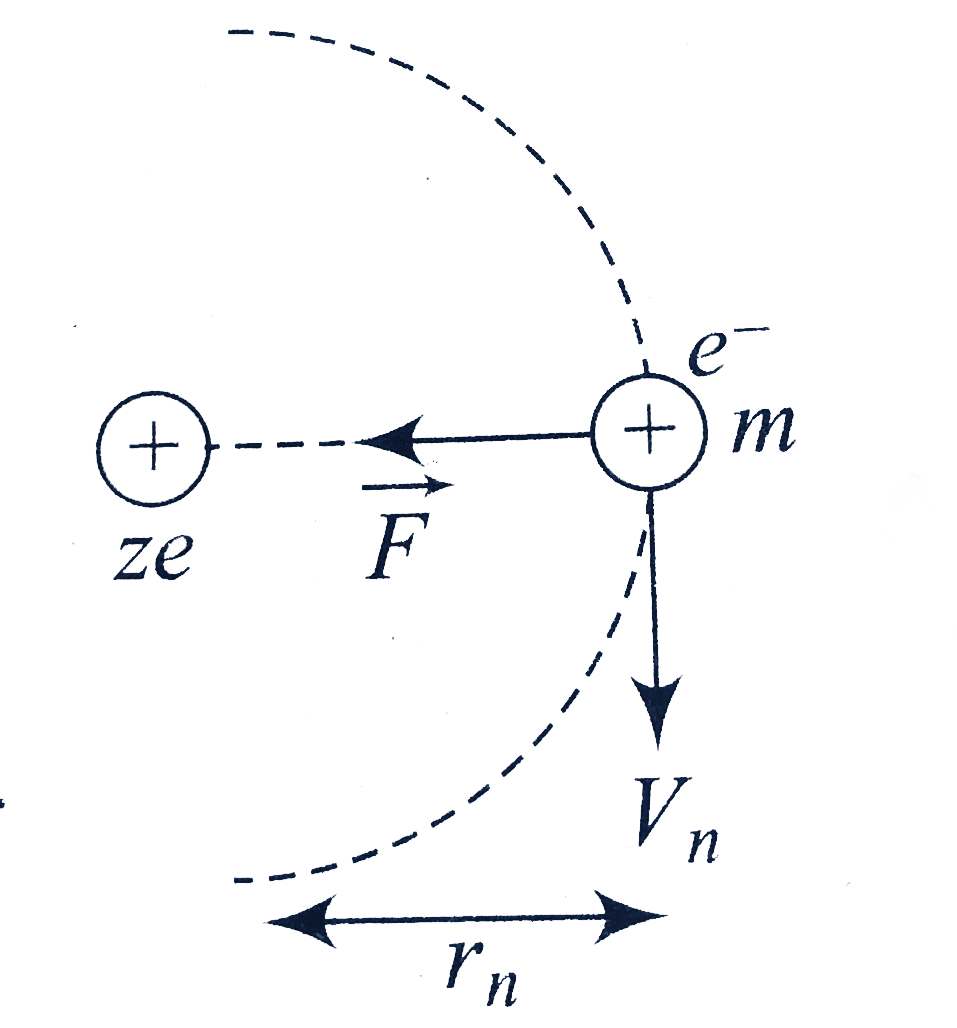
Assertion: In the duration electron jumps from fist excited state to ground state in a stationary isolated hydrogen atom, angular momentum of the electron about the nucleus is conserved.
Reason: As the electron jumps from first excited state to ground state, in a hydrogen atom, the electrostatic force on electron is always directed towards the nucleus.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will beView SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
The minimum permissible radius of the orbit will beView SolutionConsider a system containing a negatively charge poin (π,mπ=273∘me) orbital around a staionary nucleus of atomic number Z .The total energy (En) of ion is half of its potential energy (PEn) in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The longest wavelength radiation emitted in the emission spectrum when the pion de-excited from n=3 to ground state lies which of the following region ?View SolutionConsider atoms H,He+,Li++ in their ground states. If L1,L2 and L3 are magnitude of angular momentum of their electrons about the nucleus respectively then:
View Solution

